Les réseaux de neurones artificiels sont simplement des systèmes inspirés du fonctionnement des neurones biologiques. Le plus célèbre d’entre eux est le perceptron multicouche (écrit également multi-couches), un système artificiel capable d’apprendre par… l’expérience ! Introduit en 1957 par Franck Rosenblatt, il n’est véritablement utilisé que depuis 1982 après son perfectionnement. Grâce à la puissance de calcul des années 2000, le perceptron s’est largement démocratisé et est de plus en plus utilisé.
Aujourd’hui nous allons voir ensemble tout ce qui se cache derrière cet outil incroyable, puis l’utiliser de deux manières différentes : en partant de zéro puis en utilisant une librairie existante (keras et tensorflow).
Remarque : les termes anglais seront donnés pour faciliter d’éventuelles recherches sur internet.
I. La théorie derrière le perceptron multicouche
Dans cette partie nous allons voir ensemble toutes les notions derrière les réseaux de neurones en général ainsi que le perceptron (perceptron). Il faut bien noter dès à présent que le perceptron est un cas particulier de réseau de neurones, mais très souvent, quelqu’un qui dit « réseau de neurones artificiels » (artificial neural network) pense au perceptron (cas le plus simple et le plus répandu), même s’il peut s’agir d’un autre type comme par exemple un réseau de neurones convolutionnel, un réseau de neurones récurrent, etc…
1. Principe général : séparer l’espace
Le perceptron prend en entrée un vecteur à plusieurs dimensions (1 par neurone) et opère une séparation entre ces données pour fournir une sortie. Grâce à cette séparation qu’il a construite entre les données, il sait, pour un nouvel exemple, quelle doit être la réponse.
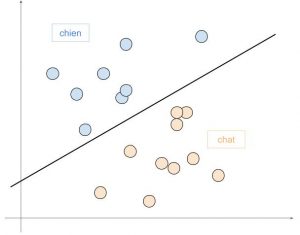
Par exemple, si on a 2 classes en sortie (chat ou chien), on va entraîner le réseau à comprendre la différence entre les deux à partir des entrées.
Le réseau se comportera ensuite comme une fonction « affine » (dans ce cas à gauche) et tracera une droite séparant les chats des chiens. Pour tout nouveau point, il aura juste à regarder de quel côté il est de la droite.
Si on ajoute des neurones, le système se complexifie et le réseau peut découper de plus en plus précisément l’espace ou même assembler des découpages !
2. Présentation générale
A l’image de la biologie, le perceptron est un ensemble de neurones organisés en couche. D’une couche à l’autre se propage le signal d’entrée jusqu’à la sortie, en activant ou non au fur et à mesure des neurones.
Le principe est de regarder la sortie par rapport à ce qui était attendu et de mettre à jour les liaisons entre les neurones (les renforcer ou les inhiber) pour améliorer notre résultat final, qui sera une prédiction de la part du réseau.
Par exemple, si vous entraînez votre réseau à estimer le prix d’un appartement à partir de sa taille, de son emplacement, et de sa consommation énergétique, vous lui donnerez des milliers d’exemples de prix. Puis pour un tout nouvel appartement, le réseau vous prédira le prix (par rapport à tout ce qu’il a déjà vu) !
a) Les couches du perceptron
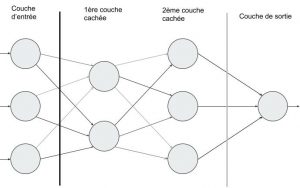
Le perceptron est organisé en trois parties :
- La couche d’entrée (input layer) = un ensemble de neurones qui portent le signal d’entrée.
Par exemple, si notre réseau essaie d’apprendre à réaliser un XOR entre 2 bits, on aura en entrée bit1 et bit2 (donc 2 neurones, un pour chaque information). Si vous voulez apprendre au réseau à estimer le prix d’un appartement, vous aurez autant de neurones que de variables… Ou bien souvent davantage (comme on le verra ensuite).
Tous les neurones de cette couche sont ensuite reliés à ceux de la couche suivante.
- La couche cachée (hidden layer) ou plus souvent LES couches cachées (couche cachée 1, couche cachée 2, …). Il s’agit du coeur de notre perceptron, là où les relations entre les variables vont être mises en exergue !
Choisir le bon nombre de neurones par couche et le bon nombre de couches est très difficile pour un data scientist et demande une certaine expérience. Toutefois, de manière générale, deux couches suffisent pour la plupart des problèmes, et aller au-delà de 6 à 10 couches entraîne très très souvent des problèmes d’overfitting (on a tellement appris qu’on ne peut plus généraliser). En pratique, on a souvent au moins autant de neurones par couche que ce qu’on avait d’entrées.
- La couche de sortie (output layer) : cette couche représente le résultat final de notre réseau, sa prédiction.
Important : de base, les neurones de la couche de sortie n’ont pas de signification particulière. C’est vous, en lui donnant des exemples, qui déterminez le rôle de chaque neurone d’entrée et de sortie. Si cela peut paraître abstrait, voici un cas pratique :
En entrée, vous donnez les pixels d’une image (toujours dans le même ordre). En sortie, vous avez deux neurones. Dans les résultats attendus, vous voulez que le premier neurone fasse 1 si l’image était un chien et 0 si c’était un chat (inversement pour le deuxième neurone : 0 et 1). Vous avez donc entraîné votre réseau en donnant comme sens au premier neurone de sortie « c’est un chien » et au deuxième « c’est un chat » ! Vous interprétez donc les valeurs de sortie (par rapport à ce que vous avez utilisé dans l’apprentissage).
un perceptron c’est 3 couches de neurones : couche d’entrée, couche(s) cachée(s), couche de sortie
b) Zoom sur un neurone
Considérons notre neurone bleu et explicitons son fonctionnement.
Des signaux \(x_0, x_1, x_2\) arrivent à notre neurone (ils viennent de la couche précédente, donc on peut en déduire qu’elle contient 3 neurones). Chaque lien qui amène le signal est pondéré, respectivement \(w_0, w_1, w_2\). C’est ce poids (weight) qui va être adapté tout au long de l’apprentissage pour permettre au réseau de prédire efficacement (en général il reste entre 0 et 1 ou -1 et 1).
Remarque sur les poids : on me demande souvent si tous les neurones doivent être reliés entre eux. La réponse est oui, mais en pratique un poids entre deux neurones peut valoir 0 : la liaison est donc représentée mais le neurone d’entrée n’a aucun impact sur le neurone considéré car \(0 \cdot x_i = 0\).
On calcule la somme de tous ces signaux pondérés (\(\sum\limits_{i=0}^{2} w_i \cdot x_i\)) et on ajoute un certain biais \(b\). Ce biais (bias) peut être vu comme un neurone externe supplémentaire qui envoie systématiquement le signal 1 de poids \(b\) au neurone bleu. Grâce à lui, la fonction d’activation va être décalée et le réseau aura donc de plus grandes opportunités d’apprentissage.
Une fois cette somme calculée, on applique une fonction d’activation (activation function) pour obtenir notre signal de sortie. Cette activation représente le seuil à partir duquel un neurone va émettre un signal (s’il a été suffisamment stimulé), et est donc lié au potentiel d’action en biologie.
- La formule de sortie d’un neurone caché sera donc toujours de la forme : \(y = f_{\text{activation}}(b+\sum\limits_{i} w_i \cdot x_i)\)
- Celle d’un neurone d’entrée sera \(y = x\) (en général on ne considère même pas qu’il y a un calcul)
- Et celle d’un neurone de sortie sera \(y = \sum\limits_{i} w_i \cdot x_i\)
Dans la pratique, les poids sont initialisés au hasard lorsqu’on crée le réseau de neurones (on détaillera les raisons par la suite). Il en va de même pour le biais. Au niveau de la fonction d’activation, pour les neurones d’entrée il n’y a pas de somme ni d’activation (on peut considérer utiliser l’identité), pour les couches cachées on a plusieurs choix (sigmoïde, reLu, …) et pour la couche de sortie, on n’applique rien directement mais on peut appliquer en dehors « softmax » (ou d’autres fonctions).
un neurone c’est : une somme pondérée de signaux, avec une fonction par-dessus
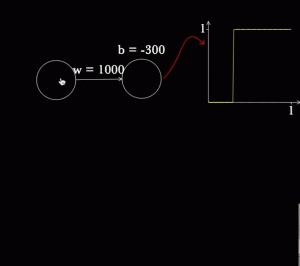
BONUS : Voici un petit outil que j’ai découvert sur CognitiveMedium, qui propose un petit projet Javascript nommé « Magic Paper » afin de pouvoir créer des neurones en dessinant et, surtout de voir la sortie du système !
Pour l’utiliser, il faut être en plein écran sur votre navigateur web d’ordinateur. Allez sur la page suivante, hébergée sur Pensée Artificielle avec le projet Github embarqué :
- Pour tracer un neurone, dessinez un rond à la souris (neurone avec sigmoïde) ou un carré (neurone avec une fonction caractéristique de l’ensemble x>0)
- Appuyez sur R pour qu’il reconnaisse chaque neurone (à faire au fur et à mesure)
- Reliez les neurones avec votre souris
- Faites deux axes (puis R) pour construire un graphe, que vous relierez à votre neurone
- Et voilà ! Vous pouvez faire varier b et w pour observer les conséquences sur votre neurone (mettez votre souris sur le neurone et appuyez sur P)
Une vidéo explicative est disponible sur Youtube :
c) Comment apprendre
La phase d’apprentissage repose intégralement sur la « descente de gradient« .
Suite à l’évaluation d’une entrée par le réseau de neurones, on peut la comparer à la réponse attendue et dire de combien est-ce qu’il s’est trompé. S’il prédit 0.7 et qu’on attendait 1, son erreur est calculée soit avec une norme \(L_1\) ou \(L_2\) ou autre (cf l’explication sur les normes).
On met alors les poids à jour un par un à partir de cet écart, en partant de la fin et en remontant. Toute cette phase sera justifiée dans la partie 5, mais on peut déjà dire qu’elle s’appuie sur… les dérivées partielles… (pour évaluer l’impact d’un changement de poids sur notre erreur).
3. Aparté sur les données et leur préparation
La donnée… on en entend tout le temps parler car il s’agit du nerf de la guerre (du machine learning). Les réseaux de neurones n’échappent pas à la règle et utilisent des milliers de lignes de données pour apprendre.
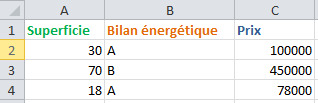
Concrètement, les données sont très souvent fournies sous forme d’un tableau CSV ou d’un fichier texte, comportant plusieurs lignes et plusieurs colonnes :
- Une colonne représente une information : la première colonne pourrait être la taille de l’appartement, la deuxième son bilan énergétique, etc… La ou les dernières colonnes représentent les données attendues en sortie, comme le prix de l’appartement
- Une ligne représente un exemple : première ligne on aura un premier appartement avec sa taille, son bilan et son prix, deuxième ligne on en aura un autre et ainsi de suite.
Pour que l’algorithme apprenne bien, il faut en général plusieurs milliers, dizaines de milliers voire millions de lignes, même si ce n’est pas une règle absolue et dépend surtout du modèle à construire.

Toutefois, les données ne doivent pas être utilisées sans un traitement préalable !
un bon algorithme est un algorithme avec de bonnes données
a) Données catégorielles (qualitatives)
Une variable catégorielle alias qualitative (et non « catégoricielle ») mesure des états ou des catégories. Par exemple, le bilan énergétique est une catégorie (A, B, C…).
Si certains voudraient remplacer A, B, C par 0, 1, 2 ou même 1, 2, 3, sachez que cette technique n’est pas bonne car il y a des mathématiques derrière qui interviennent. Or, 3 > 1, donc vous donnerez beaucoup d’importance au fait d’appartenir à la catégorie C par rapport à la 1 (votre neurone sera 3 fois plus excité !). Si on avait des catégories avec une notion d’ordre, on pourrait cependant procéder ainsi.
La solution pour contourner ce problème et mettre sur un pied d’égalité A, B, C est de traduire la colonne Bilan en 3 colonnes et de mettre un 1 dans la colonne qui contient le bilan voulu (cf tableau).
b) Données quantitatives
Ce sont des quantités : un poids, une taille, un nombre de participants, un temps…
Les données peuvent être continues (valeurs intermédiaires possibles) ou discrètes (nombres entiers).
En général, ces données doivent être traitées pour se situer entre 0 et 1. En effet, dans notre exemple, le fait d’avoir un 450 000 par rapport à un 78 000 est très impactant (on a un écart énorme entre les deux valeurs), donc le réseau va se focaliser sur avoir juste pour le 450 000 (un petit écart dessus entraîne une erreur énorme), ce qu’on veut éviter.
La solution ici est de ramener entre 0 et 1, de plusieurs manières (on choisit celle qu’on veut). Par exemple, diviser la colonne par son maximum (ce qu’on a fait ici avec le prix), passer par la moyenne de la colonne pour recentrer, etc… le choix aura de l’importance (on pourra donner plus ou moins d’importance aux valeurs extrêmes, aux valeurs médianes, etc…).
Pour des données discrètes (ou même continues), il peut être intéressant de considérer que c’est une donnée catégorielle avec des intervalles. Pour la superficie, on peut se moquer de l’information « 70m² > 30m² ». Dans ce cas, on peut découper en intervalles « de 0 à 20m² », etc… et traiter la donnée comme une donnée catégorielle. A vous de décider.
c) Les données absentes
Parfois, certaines cellules seront absentes. Ce sera également à vous de décider comment procéder. Faut-il ignorer complètement la ligne ? Faut-il mettre dans cette cellule la valeur moyenne de toute la colonne ? Faut-il y mettre une valeur particulière (inventer une nouvelle catégorie par exemple) ?
Tous ces choix impacteront évidemment les résultats de l’algorithme final, donc n’hésitez pas à expérimenter !
d) Découpage des données pour l’entraînement, les tests…
Le tableau de données est découpé (aléatoirement ou non) en 2 voire 3 parties :
- Les données d’apprentissage/d’entraînement (training set), qui vont servir à apprendre au perceptron. Cela représente en moyenne 80% des données globales
- Les données de test (test set), qui servent à évaluer les progrès de notre algorithme. Elles sont présentes à 20%
- Les données d’évaluation (evaluation set), qui sont de quelques lignes à 30% des données d’apprentissage (mais il faut les enlever AVANT d’apprendre, et la proportion dépend de la taille de notre fichier !). Ces données servent non pas à mesurer l’efficacité d’un algorithme comme le test set mais à comparer des algorithmes entre eux. Comme on l’a dit, il faut bien souvent tester plusieurs réseaux en faisant varier le nombre de couches, de neurones, d’étapes d’apprentissage, etc… Les données d’évaluation vont ainsi permettre de retenir le meilleur modèle au final.
4. Propagation de l’information, le calcul de la sortie du réseau
Si vous avez tout suivi, cette sous-partie devrait être très simple. Votre ligne de données arrive en entrée du réseau. Vous pouvez calculer la sortie de tous les neurones de la première couche cachée en appliquant la formule vue précédemment (somme avec biais puis fonction d’activation).
Avec les sorties de la première couche, vous pouvez ensuite calculer les sorties de la 2ème, puis la 3ème, et ainsi de suite jusqu’à la sortie. Votre information s’est donc propagée dans l’ensemble du réseau !
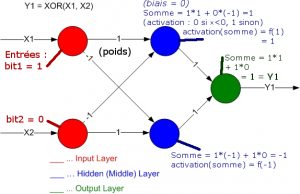
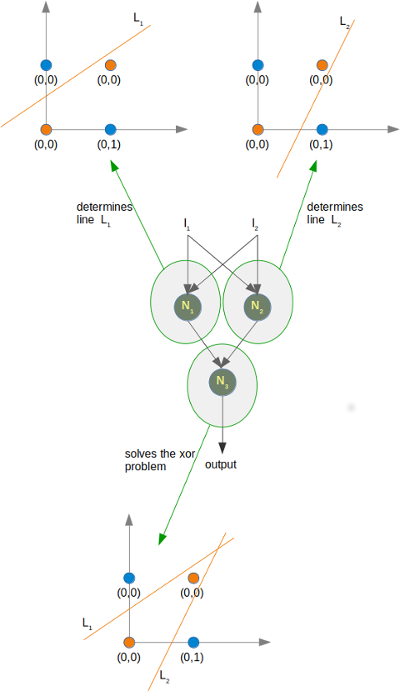
Si on prend pour exemple le XOR sur 1 couche cachée à 2 neurones, qu’on se donne en entrée 1, 0, alors avec les poids indiqués, on trouve pour la couche cachée des sorties 1 et -1, puis en sortie finale 1. Vous pourrez tester que le réseau de neurones proposé avec ces poids résout bien le XOR !
5. Rétropropagation du gradient, une manière d’apprendre par l’expérience
Parlons à présent du nerf de la guerre des perceptrons multicouches, ce qui rend possible l’apprentissage : le système de mise à jour des poids pour adapter le modèle aux données i.e. la descente de gradient.
En effet, les poids (et le biais) sont les seules variables, au final, du perceptron, un fois l’architecture mise en place (neurones, couches, vitesse d’apprentissage…).
Lorsque l’on regarde l’erreur commise par notre perceptron sur une propagation, on peut évaluer l’impact qu’a eu un poids en particulier sur cette erreur. Grâce à cette information, on peut également évaluer si augmenter ou diminuer ce poids va améliorer ou empirer notre erreur (c’est la rétropropagation du gradient).
Notre perceptron peut donc se résumer à un énorme système d’équations linéaires (avec des fonctions d’activation) dont les variables sont les poids \(w_1, w_2, …\) ! Dériver ce système (pour l’erreur) nous permet de nous diriger vers le minimum de ce système (i.e. où l’erreur est minimale).
Concrètement, en calculant la dérivée partielle de l’erreur par rapport à un poids, on obtient la pente de la dépendance de notre système en cette variable. Par exemple, si la dérivée partielle est positive, cela signifie qu’il faut diminuer notre poids pour « descendre la courbe d’erreur » et s’il est négatif, il faut l’augmenter ! La mise à jour d’un poids \(w_i\) est donc, pour \(\eta\) la vitesse d’apprentissage et \(\alpha\) la pente trouvée de l’erreur par rapport à ce poids : \(w_i := w_i – \eta \cdot \alpha\).
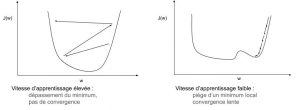
A quoi ça sert d’ajouter une vitesse d’apprentissage ?
Le problème avec la convergence, c’est qu’elle peut-être très longue à « arriver ». Si le calcul nous donne la direction et le pas à effectuer pour nous rapprocher d’un minimum du système, il y a tout d’abord un risque de tomber sur un minimum local. Si on calcule la dérivée, elle nous dira qu’on est au minimum et qu’il ne faut plus bouger nos poids (alors qu’on pourrait améliorer notre réponse). Ajouter une vitesse d’apprentissage permet de se sortir, en général, de ce type de situation (sauf si la valeur choisie est trop petite).
A l’inverse, si on choisit une valeur trop élevée, on risque de sauter d’un côté de la solution optimale à l’autre sans jamais se rapprocher (voire même en s’éloignant) !
La vitesse d’apprentissage est donc impactante pour notre perceptron, et en général on la choisit de 0.001 à 0.5. On peut également laisser cette valeur « élevée » au début (puisque nos poids sont initialisés au hasard) afin de se diriger rapidement vers la solution, puis diminuer cette vitesse pour affiner notre réponse…
Au passage, on préfère initialiser les poids au hasard pour éviter au maximum les minimas locaux. En général, on entraîne plusieurs fois un algorithme avec des poids de départ différents pour être certains de ne pas garder les solutions de type « minimum local ».
la descente de gradient permet d’évaluer l’impact d’un poids sur l’erreur et donc de s’améliorer
Pour conclure ce paragraphe, on va donner en exemple le calcul de la descente de gradient sur un perceptron à une couche (one-layer perceptron). Notre perceptron aura 2 neurones en entrée, 2 neurones sur la couche cachée et 1 en sortie.


6. Outils de mesure de notre réseau de neurones artificiels
Un premier critère est la mesure de l’erreur au cours du temps (loss function). Lorsque le réseau prédit un résultat (vecteur \(y = \left(y_1, y_2, …\right)\)) et qu’on le compare avec le résultat attendu (vecteur \(y_{\text{attendu}}\)), on peut calculer l’écart entre les deux vecteurs grâce à la norme \(L_2\) par exemple. Cette erreur est ensuite tracée et donne la courbe dite « loss function ». Cette erreur peut être calculée sur un vecteur ou sur un ensemble de vecteurs.
Les autres critères souvent regardés sont les faux-positifs et les faux-négatifs, car ils peuvent être très importants pour notre réseau. Prenons l’exemple d’un réseau qui prédit si un patient a le cancer. Avoir trop de faux-positifs revient à dire trop souvent à des patients qu’ils sont malades alors qu’il n’en est rien (un examen approfondi les rassurera mais coûtera de l’argent à l’Assurance Maladie pour « rien »). Un faux-négatif, en revanche, pourrait avoir des conséquences mortelles pour le patient, qui serait malade mais n’en saurait rien…
De même, pour les vrais-positifs, ils peuvent être plus importants que les vrais-négatifs dans le cas de la détection de fraude bancaire. Le but d’un perceptron serait de déterminer si une transaction est anormale, donc seuls les vrais-positifs nous intéresseraient véritablement.
Les résultats du réseau de neurones sont mis dans un tableau de 2 lignes 2 colonnes : la matrice de confusion. Plusieurs calculs sont possibles, et chacun a sa pertinence.
Si le calcul peut paraître laborieux, plusieurs librairies Python permettent de construire la matrice à notre place. Par exemple, avec scikit-learn :
from sklearn.metrics import confusion_matrix confusion_matrix(y_test, y_pred)
Ou avec pandas :
import pandas as pd df_confusion = pd.crosstab(y_actu, y_pred)
Et si vous voulez avoir toutes les informations sans avoir à réaliser vos calculs, pandas_ml pourrait être la solution :
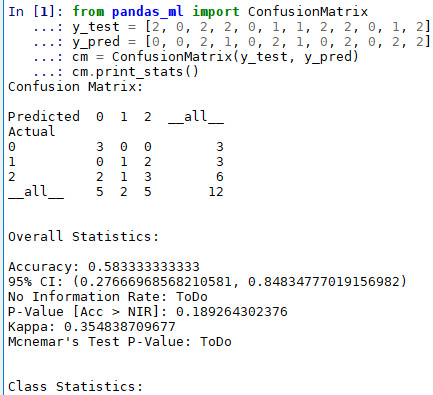
from pandas_ml import ConfusionMatrix y_test = [2, 0, 2, 2, 0, 1, 1, 2, 2, 0, 1, 2] y_pred = [0, 0, 2, 1, 0, 2, 1, 0, 2, 0, 2, 2] cm = ConfusionMatrix(y_test, y_pred) cm.print_stats()
Qui donne :
7. Pour aller plus loin
a) Overfitting
Vouloir mettre beaucoup de couches ou de neurones peut sembler une bonne idée au début. Toutefois, en augmentant le nombre de variables dans votre réseau, vous lui permettez de tracer des fonctions de séparation toujours plus précises (on peut se dire qu’on augmente la dimension de notre polynôme).
Lorsque la courbe est trop proche du jeu de données, elle obtient des score incroyables (99% !!) mais s’avère particulièrement nulle pour des prédictions qui sortent de ses jalons et on parle d’overfitting.
Il faudra donc trouver le bon équilibre, car s’il n’y en a pas assez, la séparation ne sera pas complète et on aura aussi des erreurs…
b) Fonctions d’activation
Voici quelques fonctions d’activation usuelles :
- Sigmoïde : \({\frac {1}{1+e^{-x}}}\)
- Softmax (souvent réservée à la sortie) : \(\sigma (\mathbf {z} )_{j}={\frac {e^{z_{j}}}{\sum _{k=1}^{K}e^{z_{k}}}}\)
- Rectifier Linear Unit (ReLU) : \(\max(0,x)\)
- Tangente hyperbolique : \(\tanh x={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}\)
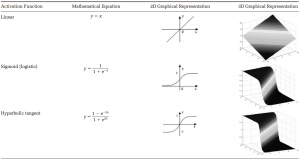
Leurs usages varient suivant vos besoins, certaines permettant d’enlever toutes les valeurs sous un certain seuil (relu décalé par rapport à 0), d’autres replacent vos valeurs entre -1 et 1 ou 0 et 1 (tanh, sigmoid), et d’autres encore transforment un vecteur en une probabilité (toutes les composantes sont ramenées entre 0 et 1 et leur somme vaut 1, avec softmax).
II. Pratique : un réseau de neurones artificiels
La théorie bien en tête, nous allons mettre en pratique ce que l’on vient de voir sur un exemple très simple et rapide, que l’on peut même résoudre avec une feuille et un stylo !
Si vous voulez télécharger directement les codes, voici le lien Github de notre repo.
1. Le problème
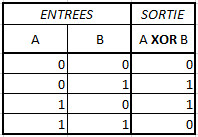
On va construire un réseau de neurones à une couche pour résoudre le problème du OU EXCLUSIF (XOR). Celui-ci prend 2 bits en entrée, A et B, puis renvoie 0 si A et B sont identiques et 1 s’ils sont égaux.
On va donc utiliser 2 neurones dans la couche d’entrée, 1 dans la couche de sortie et 1 couche cachée de 2 neurones. On rappelle que dans la partie I.4, la solution finale des poids avait été donnée (dernier schéma).
2. Construire son premier réseau de neurones à la main
On va essayer d’aller assez vite, car dans la pratique vous utiliserez plutôt des librairies toutes prêtes (keras, tensorflow…). Le code du cas pratique est tiré du lien suivant, car il est simplissime et facile à lire. Une approche orientée objet sera donnée ensuite.
a. Préparation de son environnement
Pour ce TP nous n’aurons pas besoin de grand chose :
- Télécharger Python, dans sa version 3.
- Installer les librairies suivantes, grâce à la console Windows (pour votre Python) : saisir les commandes
pip install numpy
b. Définition de nos variables
On commence par charger notre unique librairie
import numpy as np
Puis on définit nos variables d’apprentissage :
- le nombre d’époques (epoch), qui représente le nombre de fois que le perceptron va réaliser une phase d’apprentissage. Cela peut être sur une ligne ou sur N lignes à la fois suivant comment vous l’avez configuré (on dit dans le second cas qu’il s’agit d’un traitement batch, l’erreur finale étant la « somme » des erreurs).
- la taille des différentes couches
- la vitesse d’apprentissage (0.1)
epochs = 20000 # Number of iterations inputLayerSize, hiddenLayerSize, outputLayerSize = 2, 2, 1 L = .1 # learning rate
On déclare notre système, X étant les entrées et Y les sorties. On notera qu’elles doivent être face à face : X[0] a pour solution Y[0], etc… Le choix d’utiliser Numpy, une librairie de calculs a été fait pour simplifier la syntaxe et pour pouvoir utiliser des fonctions pratiques (dont le produit matriciel intégré). Avec des listes, nous aurions dû écrire nos propres fonctions.
X = np.array([[0,0], [0,1], [1,0], [1,1]]) Y = np.array([ [0], [1], [1], [0]])
Enfin, on définit notre fonction d’activation, la sigmoïde, et on initialise au hasard les poids de notre réseau de neurones :
def sigmoid (x): return 1/(1 + np.exp(-x)) # activation function
def sigmoid_(x): return x * (1 - x) # derivative of sigmoid
# weights on layer inputs
Wh = np.random.uniform(size=(inputLayerSize, hiddenLayerSize))
Wz = np.random.uniform(size=(hiddenLayerSize,outputLayerSize))
c. Propagation (phase forward)
A partir d’ici, tout va se faire dans la boucle suivante (qui est l’apprentissage complet du système). Faites bien attention à l’indentation, Python y étant sensible !
for i in range(epochs):
La propagation est simple : on calcule le produit de X par Wh (on a donc la somme de chaque neurone caché) puis on applique la sigmoïde (fonction d’activation) pour obtenir la sortie de chaque neurone de la couche cachée. Pour avoir la sortie finale, on calcule la somme de ces sorties cachées multipliée par les poids de sortie.
H = sigmoid(np.dot(X, Wh)) # hidden layer results
Z = np.dot(H,Wz) # output layer, no activation
d. Rétropropagation du gradient (phase backpropagation)
On calcule tout d’abord l’erreur :
E = Y - Z # how much we missed (error)
Puis on met à jour les poids de la couche de sortie, grâce à la formule qu’on avait trouvé auparavant.
dZ = E * L # delta Z
Wz += H.T.dot(dZ) # update output layer weights
Grâce à la seconde formule, on peut mettre à jour les poids de la couche cachée (entre l’entrée et la couche cachée donc)
dH = dZ.dot(Wz.T) * sigmoid_(H) # delta H
Wh += X.T.dot(dH) # update hidden layer weights
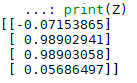
Et… voilà ! Notre réseau est complètement entraîné !
Félicitations !
e. Code complet
Voici le code complet, pour montrer à quel point il est simple
#Source : http://python3.codes/neural-network-python-part-1-sigmoid-function-gradient-descent-backpropagation/
import numpy as np
epochs = 20000 # Number of iterations
inputLayerSize, hiddenLayerSize, outputLayerSize = 2, 2, 1
L = .1 # learning rate
X = np.array([[0,0], [0,1], [1,0], [1,1]])
Y = np.array([ [0], [1], [1], [0]])
def sigmoid (x): return 1/(1 + np.exp(-x)) # activation function
def sigmoid_(x): return x * (1 - x) # derivative of sigmoid
# weights on layer inputs
Wh = np.random.uniform(size=(inputLayerSize, hiddenLayerSize))
Wz = np.random.uniform(size=(hiddenLayerSize,outputLayerSize))
for i in range(epochs):
H = sigmoid(np.dot(X, Wh)) # hidden layer results
Z = np.dot(H,Wz) # output layer, no activation
E = Y - Z # how much we missed (error)
dZ = E * L # delta Z
Wz += H.T.dot(dZ) # update output layer weights
dH = dZ.dot(Wz.T) * sigmoid_(H) # delta H
Wh += X.T.dot(dH) # update hidden layer weights
print(Z) # what have we learnt?
f. Et avec des classes ?
En Python, on peut faire de la programmation objet, pour imiter ce que proposent keras et tensorflow.
Voici un exemple d’implémentation des objets principaux. L’exercice que je vous propose (non corrigé) est de créer les fonctions suivantes :
- Forward : elle calcule, à partir d’un vecteur d’entrée, la sortie du réseau
- Backward : elle met à jour tous les poids du réseau une fois qu’une prédiction a été réalisée (et confrontée avec la « réalité »)
- Train : pendant un certain nombre d’époques et sur un jeu de données précisé, le réseau apprend
- Predict : à partir d’une entrée donne la sortie (c’est donc un Forward)
- Test : construit la matrice de confusion du perceptron à partir de prédictions
Amusez-vous bien 🙂
from random import random
class Neuron(object):
bias = 0
output = 0
weights = []
def __init__(self, prev_layer_size):
self.weights = [random() for i in range(prev_layer_size)]
def __repr__(self):
return '{"bias":"'+str(self.bias)+'" , "output":"'+str(self.output)+'" , "weights":'+str(self.weights)+'}'
class Layer(object):
activation = ''
neurons = []
outputs = []
def __init__(self, nb_neurons, prev_nb_neurons, activation):
self.activation = activation
self.neurons = [Neuron(prev_nb_neurons) for i in range(nb_neurons)]
def __repr__(self):
return '{"activation":"'+str(self.activation)+'" , "neurons":'+str(self.neurons)+' , "outputs":'+str(self.outputs)+'}'
class Network(object):
layers = []
def add(self, nb_neurons, activation='identity'):
layer = Layer(nb_neurons,
len(self.layers[-1:][0].neurons) if len(self.layers)>0 else 0, activation)
self.layers.append(layer)
def __repr__(self):
return '{"Network":{"layers":'+str(self.layers)+'}}'
Remarque : si vous voulez suivre la syntaxe de keras, il faudra créer vos fonctions dans la classe Network pour pouvoir les appeler avec « model.XXX ».
3. Construire son perceptron avec KERAS
a. Préparation de son environnement
Lancer dans la commande Windows :
pip install keras pip install numpy
b. Utilisation de KERAS pour… tout faire !
from keras.models import Sequential
from keras.layers.core import Dense, Dropout, Activation
from keras.optimizers import SGD
import numpy as np
X = np.array([[0,0],[0,1],[1,0],[1,1]])
y = np.array([[0],[1],[1],[0]])
model = Sequential()
model.add(Dense(2, input_dim=2, activation='tanh'))
model.add(Dense(1, activation = 'sigmoid'))
model.compile(loss='binary_crossentropy', optimizer=SGD(lr=0.1))
model.fit(X, y, batch_size=1, nb_epoch=500)
print(model.predict_proba(X))
for layer in model.layers:
weights = layer.get_weights()
print(weights)
model.save_weights("model.h5")
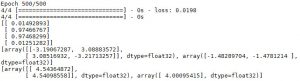
On voit que keras nous donne beaucoup d’opportunités de changer le modèle. Keras est très performant et facile d’utilisation (contrairement à TensorFlow qui a plus de fonctionnalités poussées mais s’avère donc compliqué pour un cas simple comme le perceptron multicouches).
4. Construire son perceptron avec TensorFlow !
a. Préparation de l’environnement
Lancer dans la commande Windows :
pip install tflearn
b. Le code
"""
Source : https://towardsdatascience.com/tflearn-soving-xor-with-a-2x2x1-feed-forward-neural-network-6c07d88689ed
"""
from tflearn import DNN
from tflearn.layers.core import input_data, dropout, fully_connected
from tflearn.layers.estimator import regression
#Training examples
X = [[0,0], [0,1], [1,0], [1,1]]
Y = [[0], [1], [1], [0]]
input_layer = input_data(shape=[None, 2]) #input layer of size 2
hidden_layer = fully_connected(input_layer , 2, activation='tanh') #hidden layer of size 2
output_layer = fully_connected(hidden_layer, 1, activation='tanh') #output layer of size 1
#use Stohastic Gradient Descent and Binary Crossentropy as loss function
regression = regression(output_layer , optimizer='sgd', loss='binary_crossentropy', learning_rate=5)
model = DNN(regression)
#fit the model
model.fit(X, Y, n_epoch=5000, show_metric=True);
#predict all examples
print ('Expected: ', [i[0] > 0 for i in Y])
print ('Predicted: ', [i[0] > 0 for i in model.predict(X)])
model.get_weights(hidden_layer.W)
model.get_weights(output_layer.W)
model.save("tflearn-xor")

On a choisi de vous fournir ce modèle car TensorFlow est la bibliothèque (par Google) la plus utilisée.
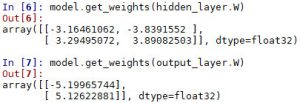
On voit qu’il y a certaines particularités (pour récupérer les poids par exemple ou dans le modèle sauvegardé), et que l’on a utilisé la tangente hyperbolique (pour changer).
III. Conclusion
Au travers de ce très long focus on a pu aborder une grande partie de problématiques et de vocabulaire de machine learning/data science. Vous avez pu découvrir et comprendre le fonctionnement du perceptron multi-couches, le réseau de neurones artificiels le plus « simple » et pratique.
Merci pour votre attention, si vous avez des remarques ou des corrections à apporter n’hésitez pas à le faire savoir dans les commentaires ! Toute l’équipe de Pensée Artificielle espère sincèrement vous avoir apporté quelque chose 🙂
Si vous voulez d’autres problèmes, voici celui du diabète et des graines.
Crédit de l’image de couverture : geralt – Pixabay License




[…] Il nous faut également choisir une fonction de coût, qui servira à quantifier l’écart entre notre prédiction et la valeur attendue. De manière traditionnelle, on va recourir à la cross-entropy avec softmax (qui transforme les valeurs de sortie en probabilité). Il faut aussi indiquer quel algorithme de mise à jour des poids on va utiliser, soit ici la descente de gradient vue dans le focus sur le perceptron. […]
[…] L’objet premier de cet article était de découvrir ensemble à quoi ressemble, concrètement, trois neurones connectés dans un perceptron. […]
[…] Ensuite, il donnera la probabilité que cette image représente un robot, un chien, un humain… grâce à un « réseau de neurones artificiels » (autre type de réseau, que l’on a déjà étudié dans le focus sur le perceptron). […]
[…] focus, vous connaissez déjà l’architecture de l’ARS : il s’agit d’un réseau de neurones artificiels (ANN) à 1 couche d’entrée 0 couches cachées et 1 couche de sortie […]
[…] Pour plus de détails sur le fonctionnement de l’ANN, je vous invite à lire notre article sur le perceptron multi-couches. […]
[…] Network) est un réseau de neurones très répandu en deep learning. Ressemblant grandement au réseau de neurones artificiels (abrégé en ANN), il est conseillé de connaitre ce dernier pour bien saisir les explications du […]
[…] Rappelons que pour chaque neurone, les signaux qui arrivent sont pondérés par les poids des liaisons et sommés (si besoin, n’hésitez pas à vous référer au tutoriel sur le perceptron). […]