Les fonctions d’activation, simulacre de transfert électrique entre synapses, des réseaux de neurones jouent un rôle déterminant dans les prédictions de ces derniers.
Pourtant, il est très rare de sortir du trio « ReLU », « tanh » et « sigmoïde ». Et si je vous disais qu’en utilisant Mish, inspirée des travaux de Google Brain, vous pourriez grappiller quelques pourcents de précision supplémentaires ?! Regardons ensemble Mish vs ReLU pour vos projets.
Un vaste choix de fonctions d’activation
Avant de s’attaquer à Mish, commençons par un panorama global des fonctions d’activation. N’hésitez pas à ignorer ce paragraphe si vous êtes familier de ces dernières…
Qu’est-ce qu’une fonction d’activation ?
Une fonction d’activation est une fonction mathématique (comme par exemple la fonction « cosinus » ou « racine carré ») qui intervient dans tous les neurones d’un réseau de neurones (artificiels, convolutifs, récurrents, etc…).
Rappelons que pour chaque neurone, les signaux qui arrivent sont pondérés par les poids des liaisons et sommés (si besoin, n’hésitez pas à vous référer au tutoriel sur le perceptron).
A quoi sert une fonction d’activation ?
Quelles sont les caractéristiques d’une fonction d’activation ? Que se passerait-il si on l’enlevait ? Chaque neurone calculerait la somme pondérée des signaux entrants :
- Mettre bout à bout des neurones donnerait, en sortie finale du réseau, une combinaison linéaire des données de la couche d’entrée, par exemple \(i_1 \cdot (w_3 + w_5 ) + i_2 \cdot (w_2 \cdot w_7 + w_3 + w_9 ) + i_3 \cdot (w_1 + w_4 ) \cdot (w_6 + w_7) \).
- La conséquence directe est que le réseau ne peut représenter efficacement que des données linéairement dépendantes (et donc on limite l’utilisation de notre intelligence artificielle)
- En outre, les fonctions d’activation sont souvent bornées i.e. elles ne peuvent pas dépasser une certaine valeur : cela évite les grands calculs et la mémoire consommée. Par exemple, si on donne la valeur 100 à la fonction d’activation tanh on obtient la nouvelle valeur 0.999 : on a, pour tout réel x, -1 < tanh(x) < 1.
A noter que toutes les fonctions d’activation ne cassent pas la linéarité, ni qu’elles sont toutes bornées. Mais elles ont alors d’autres particularités souhaitables ou non suivant les cas d’utilisation !
Quelques exemples de fonctions d’activation

ReLU
Il s’agit de l’une des fonctions les plus puissantes et les plus utiles :
- Elle est rapide/simple à calculer
- Elle casse la linéarité des valeurs négatives
- Elle désactive certains neurones
- Par contre elle n’apprend pas très vite et n’est pas bornée
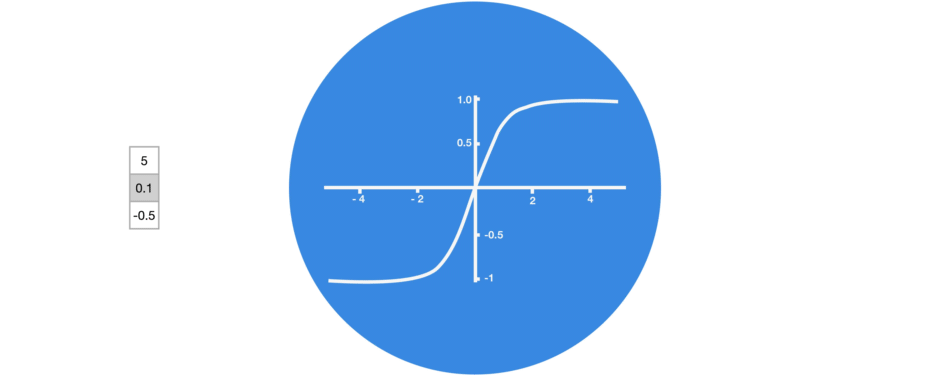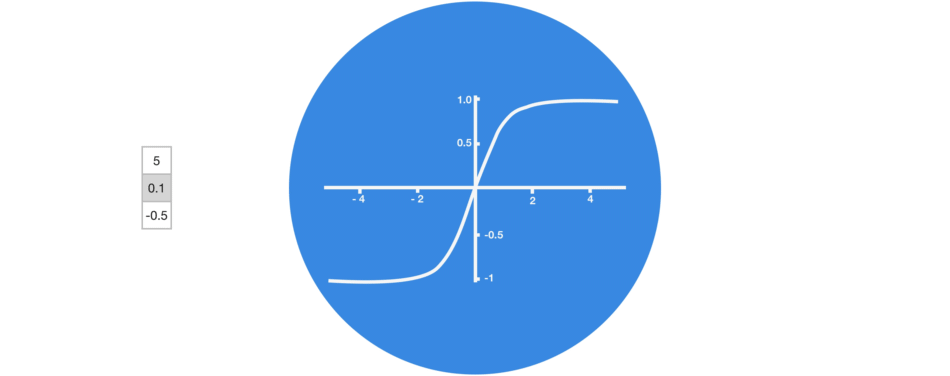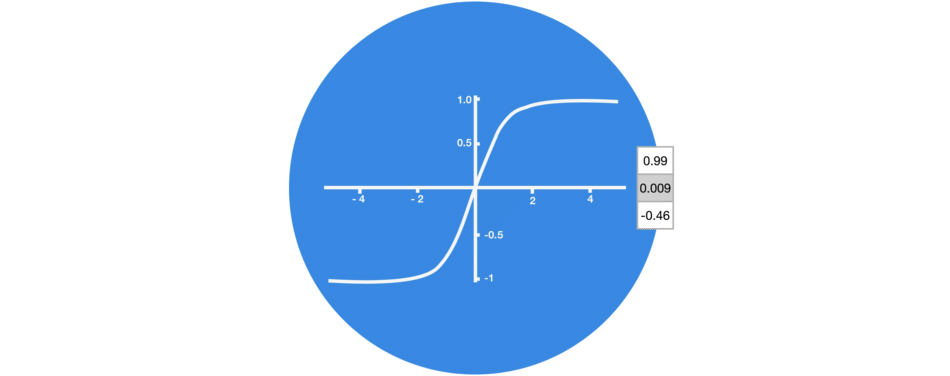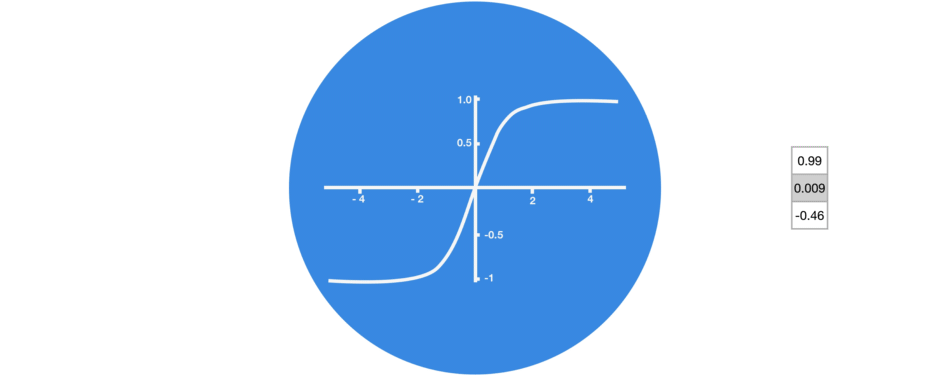
tanh
La tangente hyperbolique est la seconde fonction d’activation la plus utilisée :
- Elle ne tue pas certains neurones comme ReLU
- Elle permet de borner les valeurs
- Elle est « anti-symétrique »
- Par contre elle est plus lente à calculer
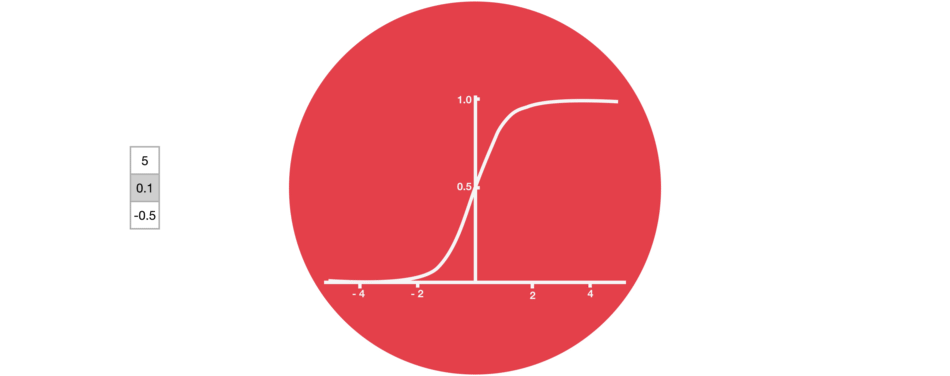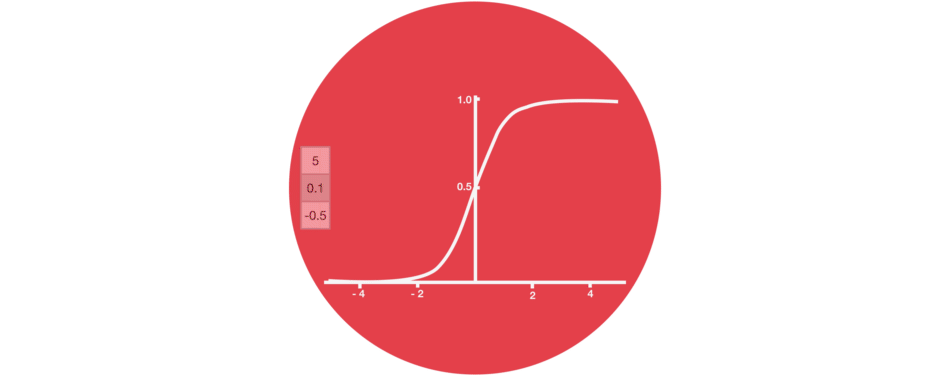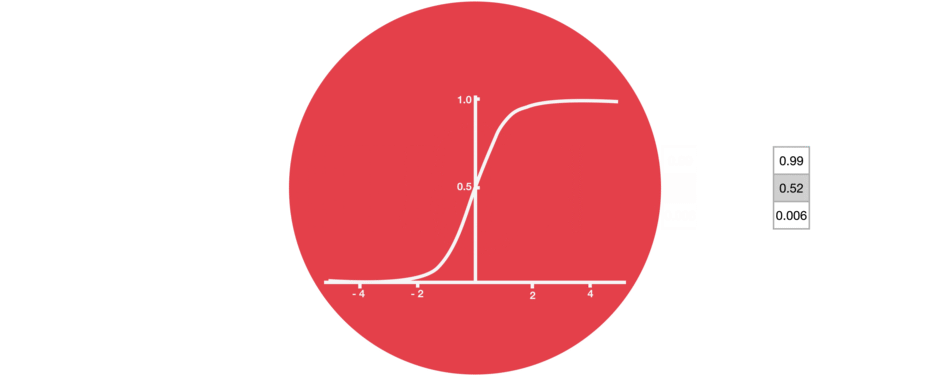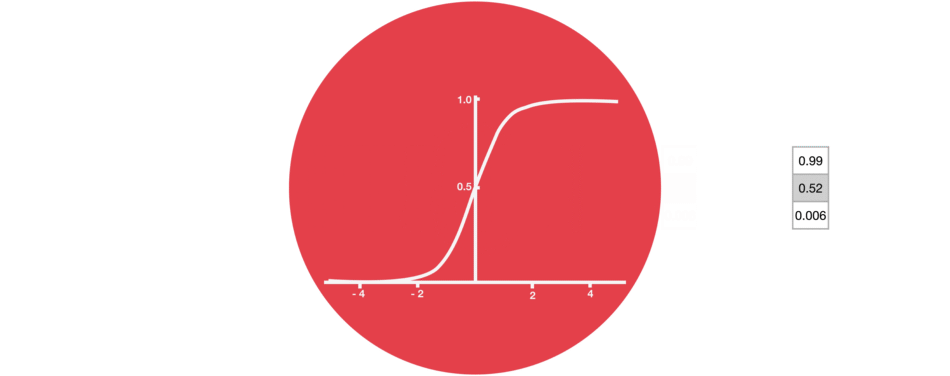
sigmoïde
Proche de la notion de probabilité, cette fonction est moins utilisée que tanh mais garde un intérêt pour ses valeurs toutes positives
Il existe des dizaines de fonctions d’activation possibles. N’hésitez pas à consulter le site de David Sheehan pour en visualiser un grand nombre !
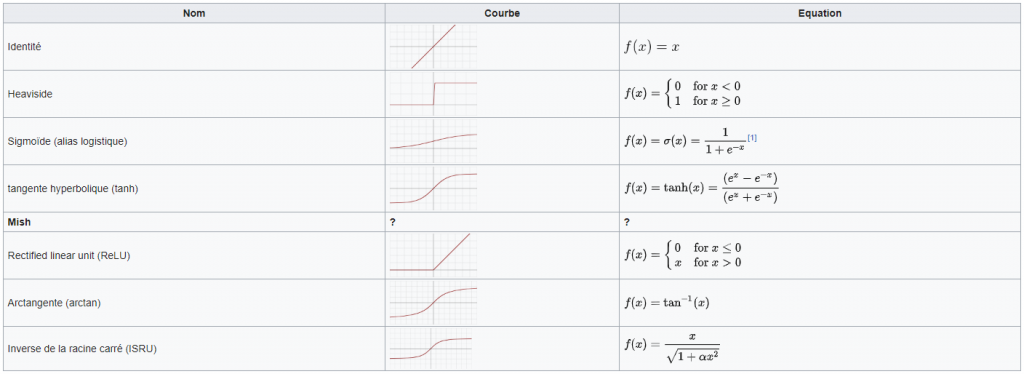
Qu’en est-il de Mish ? Comment se définit la fonction d’activation Mish ?
Mish est présentée comme une fonction auto-régularisée, non-monotone. Elle est inspirée des travaux de l’équipe de Google Brain qui a créé « Swish » en 2017, une autre fonction d’activation légèrement différente (et moins performante, d’où un article sur Mish) ! Mish a été inventée et codée par le mathématicien Diganta Misra, que je remercie pour les ressources mises à disposition. D’ailleurs, un article est disponible sur Arxiv.
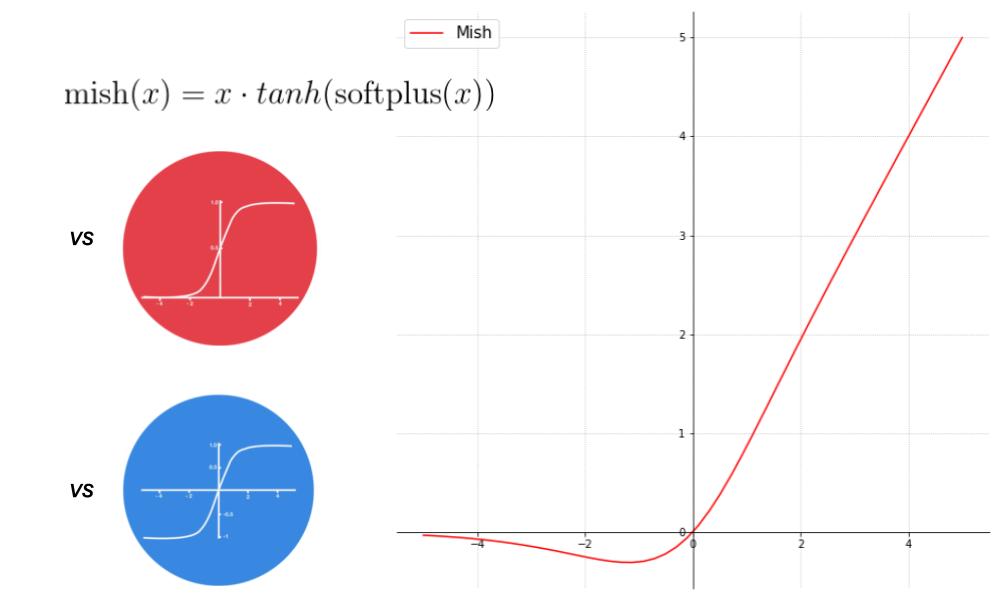
Voici le graphe de la fonction Mish :
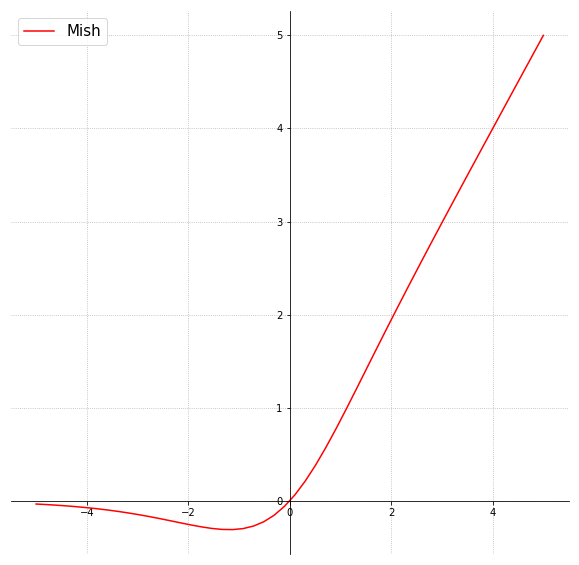
Mathématiquement parlant, Mish est une savante combinaison de tangente hyperbolique (vue précédemment), du logarithme népérien (« ln ») et de l’exponentielle (« e ») : \( \text{mish}(x) = x \cdot tanh(ln((1+e^x)) \)
A noter que \(ln(1+e^x)\) est souvent appelée fonction « softplus« , transformant la définition de Mish en \( \text{mish}(x) = x \cdot tanh( \text{softplus}(x)) \)
L’intuition derrière Mish est double. Tout d’abord, le plus gros problème de ReLU est que la fonction est nulle sur les valeurs négatives. Dans la phase d’apprentissage du réseau, cela conduit à la désactivation (on parle de neurones morts) de près de 40% des neurones en général, ce qui fait qu’ils n’apprennent rien, et donc que le système est lent à converger vers une solution. Mish, pour sa part, valorise les valeurs négatives proche de zéro mais continue de réduire l’importance des valeurs négatives ensuite (ce qui permet de mieux casser la linéarité, et de contrôler les calculs).
Ensuite, dans sa partie positive, Mish tend vers l’infini à l’inverse de tanh. L’intérêt ici est que, pour tanh, il n’y a aucune différence entre une entrée valant 100 et une entrée valant 10000000 : toutes les deux vaudront (quasiment) 1 après tanh. Il y a donc une « perte d’information » avec tanh, on parle de saturation des valeurs (ou de cap).
Enfin, il semblerait (au-delà de Mish) que les fonctions d’activation infiniment dérivables (on parle de classe C infini : \(C^{\infty}\) ou de smoothness en anglais) propagent mieux l’information dans les réseaux de neurones et obtiennent de meilleurs résultats. Par exemple, ReLU n’est pas continûment différentiable et sa dérivée seconde devient 0.
Quelle différence avec swish ? Mish vs Swish
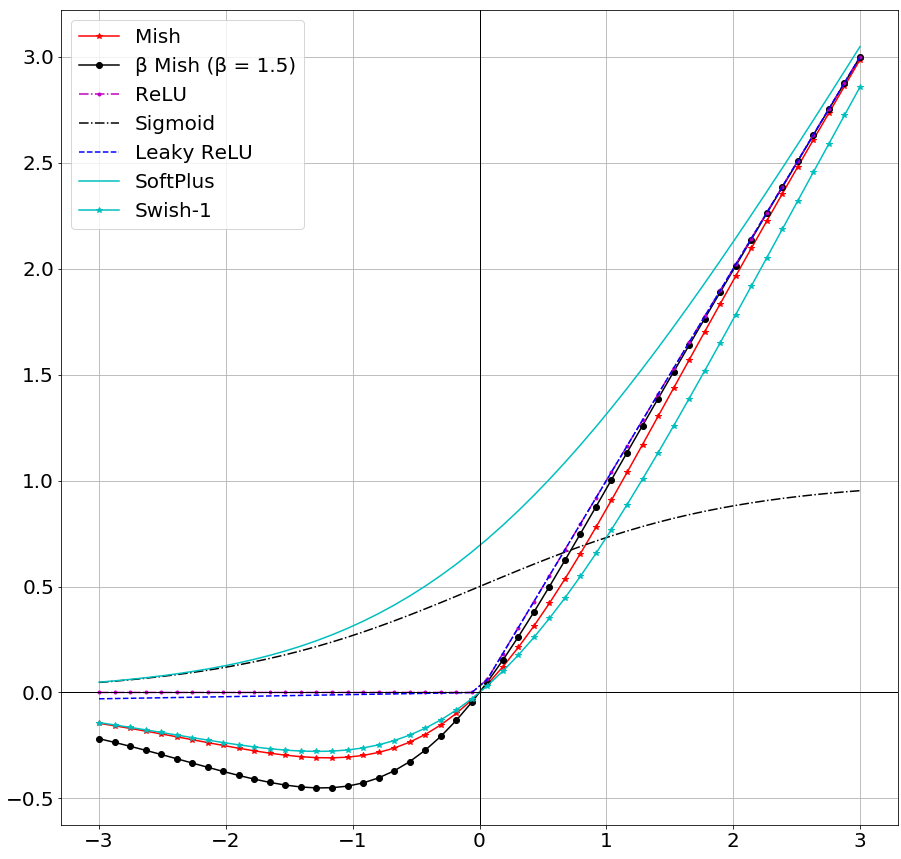
Tout d’abord, swish (qui est β-swish avec β=1) est définie ainsi :
\( \beta\text{-swish}(x, \beta ) = x \cdot sigmoid(x \cdot \beta)\)Tandis que mish (qui est β-mish avec β=1) se définit de la manière suivante :
\( \beta\text{-mish}(x, \beta ) = x \cdot tanh(ln((1+e^x)^\beta) \)En apparence plus compliquée, les deux formules donnent quasiment la même courbe, avec quelques différences au niveau de la partie négative (on a une concavité plus importante avec mish) et la pente de la partie positive.

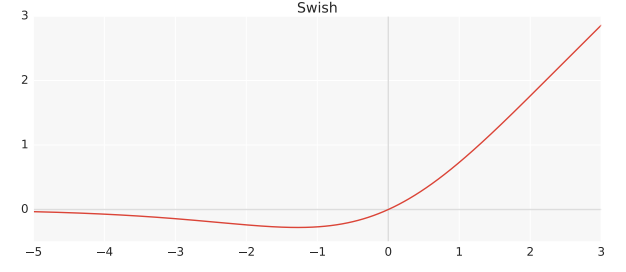
Dans la pratique, cette différence de formulation entre les deux fonctions permet à Mish d’être un petit peu plus performante : sur 75 modèles différents d’intelligence artificielle entraînés pour de la classification d’image, Mish a battu Swish dans 53 cas et a battu ReLU dans 55 cas, avec parfois 3 à 5% d’amélioration !! A noter, cependant, que Mish est la fonction d’activation la plus lente à calculer.
Concrètement, sur le jeu de données CIFAR-10, avec un réseau ResNet v2-56, la précision de Mish en 50 époques a été de 87.18% alors que celle de Swish 86.36% et de ReLU 83.86%…
Quelle est la meilleure fonction d’activation ? Mish vs ReLU
On vient de le dire juste avant : Mish a permis à notre intelligence artificielle (un réseau ResNet v2-56) de passer de 83.86% de précision sur CIFAR-10 à 87.18%, soit +3.32%.
Pourtant, comme vous le verrez en fin d’article, il y a des cas dans lesquels ReLU ou même Swish sont meilleurs que Mish. Que peut-on en conclure ? Quelle est la meilleure fonction d’activation ? Que vaut Mish vs ReLU ?
Une étude comparative a été réalisée et permet de conclure en fonction des hyper-paramètres de l’algorithme. Car oui, le podium change suivant qu’il y a plus ou moins de couches de neurones, que vous avez une vitesse d’apprentissage élevée ou non, etc… !
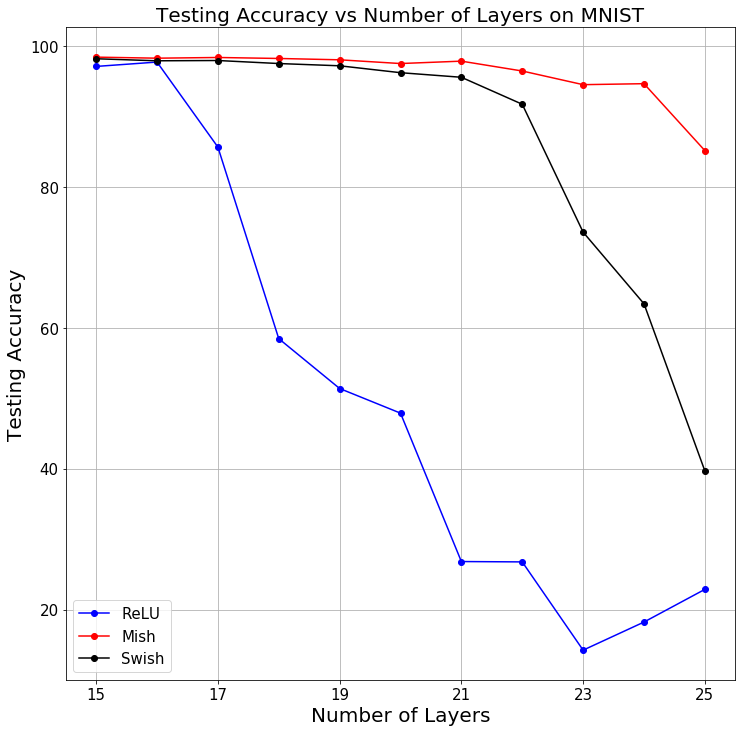
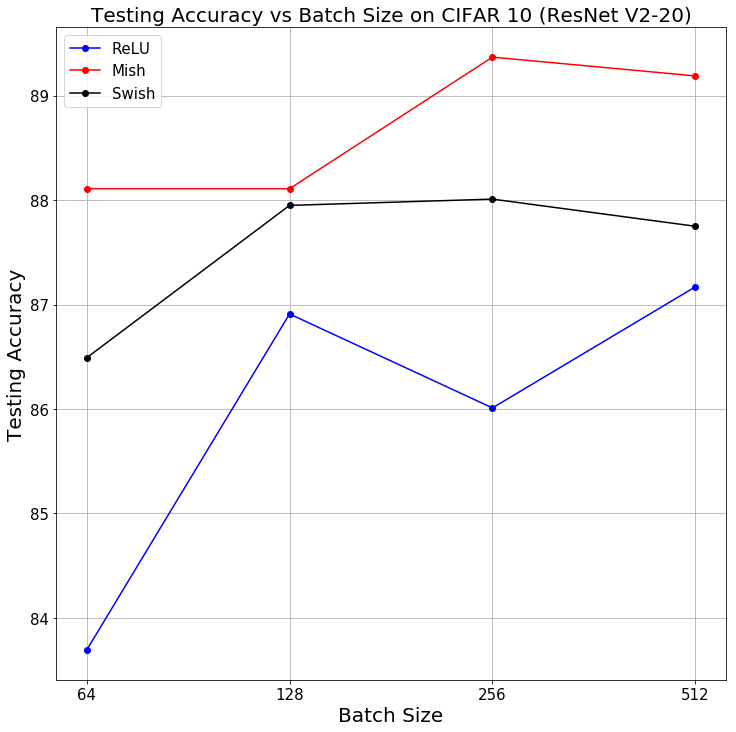
Tous ces résultats ont été compilés pour vous permettre de choisir la meilleure fonction d’activation. Voici les critères pour lesquels Mish obtient le plus haut score de prédiction sur les données d’entraînement (ces critères sont basés sur les résultats de MNIST et CIFAR-10, ils sont donc à prendre avec des pincettes). Dans les cas où Mish n’est pas favorite, Swish l’emporte.
Attention toutefois : si les critères sont trop « petits » (par exemple peu de neurones ou de couches), ReLU est généralement plus efficace.
| Paramètre | Critère |
| Nombre de couches de neurones | > 15 |
| Taille du batch | > 64 |
| Optimizers | Tous sauf Nadam |
| Vitesse d’apprentissage | < 0.1 voire 1 |
| Initializers | Tous (sauf random_normal) |
| Regularizers | l1, l2, l1_l2 |
| Dropout | Tout |
| Nombre de neurones Dense | > 100 |
| Augmentation des données | Tout |
| Mixup | Tout |
Conclusion : pour toute intelligence artificielle dont le modèle est complexe (de nombreuses couches de neurones, ou une architecture importante avec des batchs larges par exemple), Mish est la fonction d’activation qui obtient les meilleures performances. Il est donc vivement conseillé d’au-moins l’essayer dans vos entraînements et de comparer !
Mise en application : utilisons Mish dans nos projets
La fonction d’activation Mish (ainsi que β-mish) est disponible sur le Github de Diganta Misra. Celle-ci est implémentée en Keras, MXNet, Tensorflow et PyTorch.
REMARQUE : il existe une version spécialement optimisée pour CUDA de Mish. Contrairement à la version classique de Mish que nous avons vu dans cette article, Mish-CUDA utilise, lors de la rétro-propagation, des noyaux CUDA accélérés (accelerated CUDA kernels) plutôt que le système automatique différentiel du GPU de PyTorch. Cette version accélérée fonctionne uniquement sur PyTorch et est disponible dans github. N’hésitez pas à l’utiliser, elle « corrige » donc le seul éventuel problème de Mish.
Voici le code de chacune des versions.
Keras
import keras.backend as K
def mish(x):
return x*K.tanh(K.softplus(x))Tensorflow
import tensorflow as tf
def mish(inputs):
return inputs * tf.math.tanh(tf.math.softplus(inputs))PyTorch
import torch
import torch.nn.functional as F
def mish(input):
return input * torch.tanh(F.softplus(input))MXNet
import mxnet as mx
import mxnet.ndarray as F
def hybrid_forward(self, x):
return x * F.tanh(F.activation(data = x, act_type = 'softrelu'))Un framework qui inclue Mish : EchoAI
Enfin, il est bon de noter qu’EchoAI dispose de Mish dans ses versions Keras, Tensorflow et PyTorch, donc si vous utilisez la dépendance (via pip install echoai) vous pouvez appeler Mish. Remarque : Mish se développe rapidement et devrait bientôt être intégrée nativement dans Tensorflow, avant de rejoindre les autres framework.
# Exemple de code basé sur EchoAI
### PyTorch
import torch
from echoAI.Activation.Torch.mish import Mish
import echoAI.Activation.Torch.functional as Func
input = torch.randn(2)
m = Mish()
output = m(input)
print(output)
### Keras
from echoAI.Activation.Keras.custom_activations import Mish
X = Mish()(X)Exemple d’utilisation dans un projet : Mish vs ReLU
Pour pouvoir utiliser une fonction d’activation dans un réseau de neurones, il ne suffit pas d’avoir la définition de celle-ci mais il faut déclarer certaines classes et réaliser les bons imports. Utilisons Mish dans un projet Keras très simple (présenté dans le tutoriel sur le perceptron), facilement adaptable à Tensorflow, PyTorch ou MXNet.
NB : je suis en train de voir pour que l’installation soit plus simple, grâce à un pip install. L’article sera mis à jour lorsque ce sera bon !
1) Commençons par télécharger le code de Mish depuis le github sur notre ordinateur
2) Placer dans le répertoire de votre projet le fichier Mish du framework que vous utilisez (avec éventuellement le fichier functional s’il y est). Par exemple dans notre cas, prendre « mish.py » qui est dans « Mish/Keras » et le placer avec notre fichier de code de l’algorithme
3) Ajouter l’import suivant pour pouvoir utiliser dans le réseau activation= »Mish » au lieu, par exemple, de activation= »relu » :
from mish import Mish as mish
# ... #
model.add(Dense(2, input_dim=2, activation='Mish'))Voici le code complet dans lequel on utilise Mish :
from keras.models import Sequential
from keras.layers.core import Dense, Dropout, Activation
from keras.optimizers import SGD
import numpy as np
# Mish Import : needs mish.py from Mish/Keras in the same folder as this file
from mish import Mish as mish
X = np.array([[0,0],[0,1],[1,0],[1,1]])
y = np.array([[0],[1],[1],[0]])
model = Sequential()
# Using Mish activation function in a layer :
model.add(Dense(2, input_dim=2, activation='Mish'))
model.add(Dense(1, activation = 'sigmoid'))
model.compile(loss='binary_crossentropy', optimizer=SGD(lr=0.1))
model.fit(X, y, batch_size=1, nb_epoch=500)
print(model.predict_proba(X))Pour comparer Mish vs ReLU c’est très simple : remplacez ‘Mish’ par ‘relu’ et constatez par vous-même la différence (attention, le code ci-dessus est très simple et comme nous l’avons vu dans le tableau précédent, les écarts ne sont pas flagrants : essayez d’ajouter quelques couches, quelques neurones et augmentez le batch_size)…
Vers les sommets avec β-Mish !
Pour conclure cette découverte de Mish, il faut signaler l’existence d’une version β de Mish, sobrement nommée β-mish. Comme dans beaucoup de versions β, celle-ci ajoute un paramètre supplémentaire qui va permettre de gérer la pente de Mish.
\( \beta\text{-mish}(x, \beta ) = x \cdot tanh(ln((1+e^x)^\beta) \)On a alors mish = β-mish si et seulement si β = 1.
En termes d’efficacité, l’étude de Diganta Misra porte sur le cas β = 1.5 mais on peut prendre n’importe quelle valeur. Comparons les résultats obtenus pour β-Mish par rapport à ReLU, Swish et Mish.
| Dataset | Architecture | Score ReLU | Score Swish | Score Mish | Score β-Mish ( β = 1.5) |
| MNIST | LeNet-4 | 98.65% | 98.42% | 98.64% | 98.45% |
| Fashion-MNIST | Mini VGG | 93.19% | 93.09% | 93.31% | 93.44% |
| CIFAR-10 | ResNet v1-20 | 91.5% | 91.95% | 91.81% | 91.75% |
| ResNet v1-32 | 91.78% | 92.3% | 92.29% | 92.49% | |
| ResNet v2-20 | 91.71% | 91.61% | 92.02% | 92.15% | |
| Inception ResNet v2 | 82.22% | 84.96% | 85.21% | 84.83% | |
| Capsule Network | 82.19% | 82.48% | 83.15% | 83.15% | |
| CIMCD | U-Net (loss) | 0.578% | 0.639% | 0.097% | 0.144% |
| TOTAL | 1 | 1 | 3 | 4 |
Les résultats parlent d’eux-même, que ce soit Mish vs ReLU ou β-Mish vs ReLU, ReLU ne gagne (de très peu) que sur l’architecture simple de LeNet-4…
Crédit de l’image de couverture : image modifiée de Michaël Nguyen et Diganta Misra

![Spark 3 : à la découverte des RDD [Part 2]](https://penseeartificielle.fr/wp-content/uploads/2022/02/fire-1905608_1280-218x150.jpg)
![Installation de Spark 3 sous Windows [Part 1]](https://penseeartificielle.fr/wp-content/uploads/2022/02/pexels-fabiano-rodrigues-1662298-218x150.jpg)
