Les réseaux de neurones récurrents (RNN) sont largement utilisés en intelligence artificielle dès lors qu’une notion temporelle intervient dans les données (parfois « cachée » comme dans l’analyse de texte).

Mais ces derniers souffrent dans leur structure interne de limitations qui les rendent inopérants dans beaucoup de situations. Interviennent alors les cellules LSTM et GRU dont les performances n’ont d’égales que leur complexité !

Essayons d’avoir, grâce à ce guide, une compréhension simple, profonde et illustrée de comment ils fonctionnent.

Le problème des réseaux de neurones récurrents (RNN)

Comment fonctionne un RNN ?

Un réseau de neurones récurrents (RNN pour Recurrent Neural Network) est un réseau de neurones très répandu en deep learning. Ressemblant grandement au réseau de neurones artificiels (abrégé en ANN), il est conseillé de connaitre ce dernier pour bien saisir les explications du RNN.

Pour les lecteurs et les lectrices qui ignoreraient la manière dont procède un ANN, voici un bref résumé :

  • Des données d’entrées (input) arrivent dans la couche d’entrée du réseau. Les données sont sous la forme d’un vecteur, par exemple (0.7, 0.4, 0.9) et chaque coordonnée du vecteur est envoyée à un neurone jaune ci-dessous
  • Ensuite, les 3 valeurs vont avancer dans le réseau couche par couche (1ère bleue puis 2nde bleue puis orange qui est la sortie). Les couches bleues sont dites cachées et la orange dite couche de sortie.
  • Pour avancer, entre chaque neurone il y a un trait qui les relie : ce trait est associé à une valeur dite le poids (par exemple 0.3 entre le 1er neurone jaune et le 1er bleu) qui va pondérer la valeur entrante (i.e. on aura 0.7*0.3 = nouvelle valeur qui arrive dans le 1er neurone bleu).
  • Toutes les valeurs entrantes (et pondérées) sont additionnées à l’entrée d’un neurone puis on applique une certaine fonction au résultat, ce qui donne une valeur de sortie pour chaque neurone
  • Ces valeurs sont ensuite propagées à la couche suivante et ainsi de suite
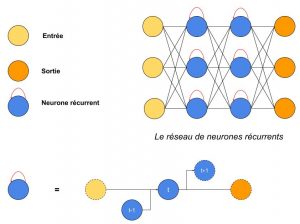
Architecture d’un réseau de neurones récurrents (crédit : Lambert Rosique)

Voici à présent le schéma d’un RNN. Contrairement à un ANN (et c’est là la seule différence), sur chaque neurone bleu, on a une boucle (développée sous le schéma du réseau) :

  • on a une donnée t (3 valeurs, une pour chaque neurone jaune) qui arrive dans le réseau
  • celles-ci se propagent dans le réseau comme dans un ANN
  • sauf que chaque neurone bleu, en plus de recevoir les sorties pondérées des neurones précédents, reçoit également la valeur qui sortait de lui-même pour la donnée t-1
  • la valeur de sortie de chaque neurone bleu est conservée et servira pour la donnée t+1

On a donc une mémoire de 1 itération pour les neurones bleus.

Voici une vision plus animée des RNN, maintenant que vous en avez l’idée principale. Partons sur l’utilisation d’un RNN pour analyser les mots de la phrase « Hier soir j’ai mangé un hamburger et des  » et prédire le mot suivant (« frites »).

Tout d’abord, chaque mot est transformé en un vecteur. Par exemple, « hier » devient (0.1, 0.5, 1) : cette transformation est une étape de préparation des données indispensable. Chaque vecteur est ensuite envoyé à tour de rôle dans le RNN, représenté ci-dessous sous la forme d’un carré vert (qui représente sa cellule i.e. un neurone).

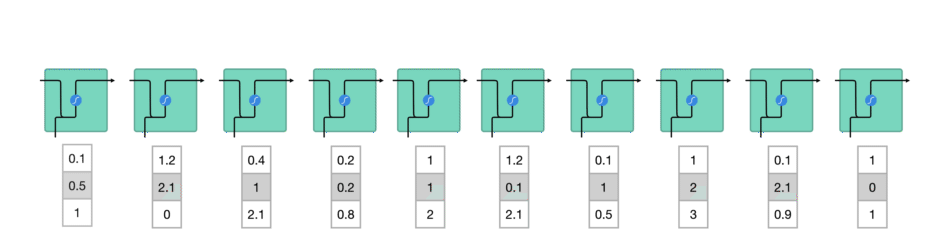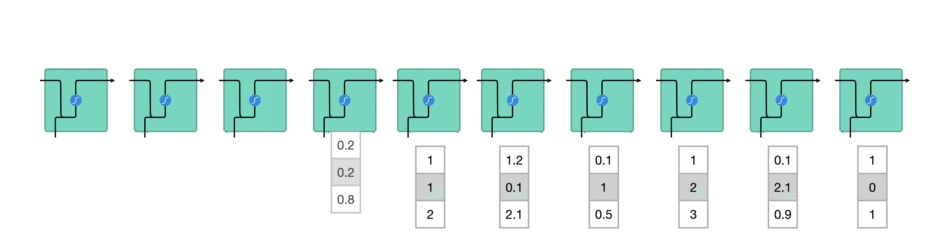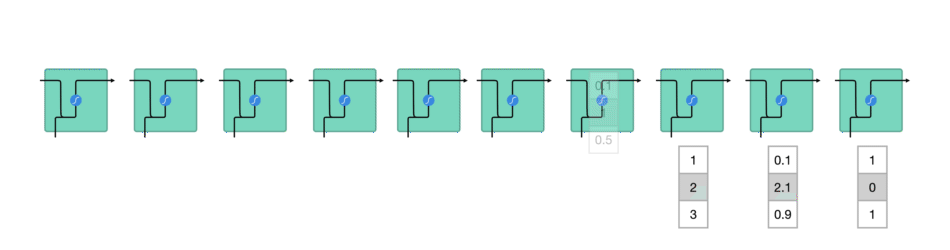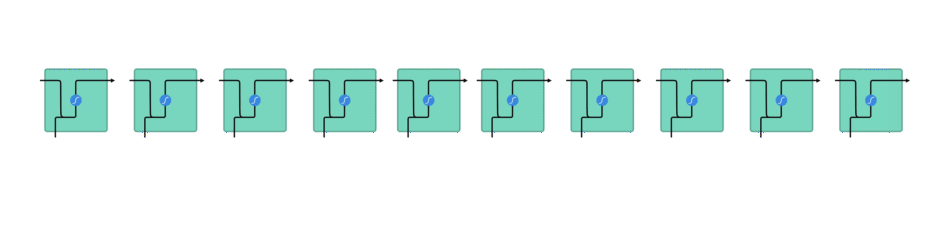
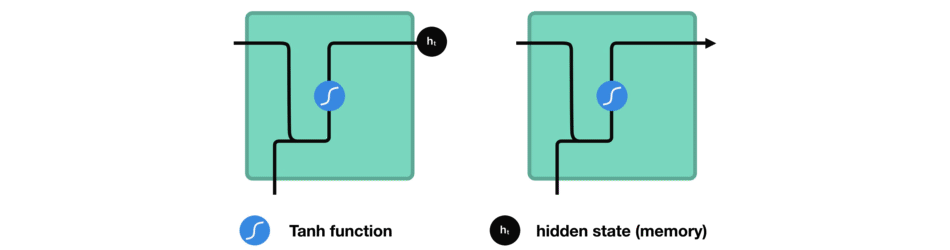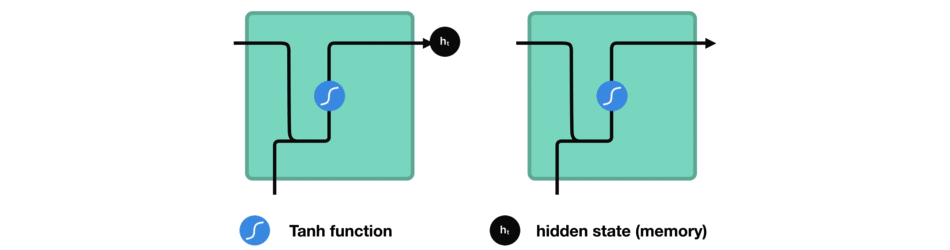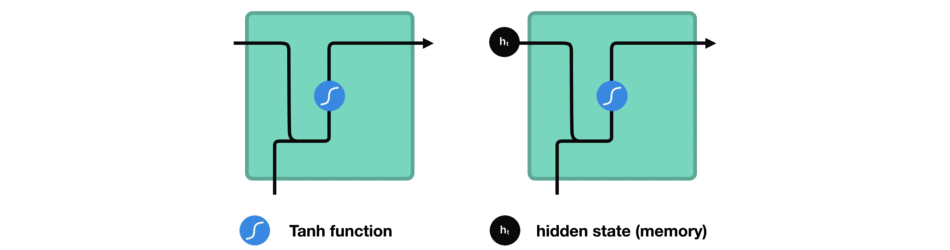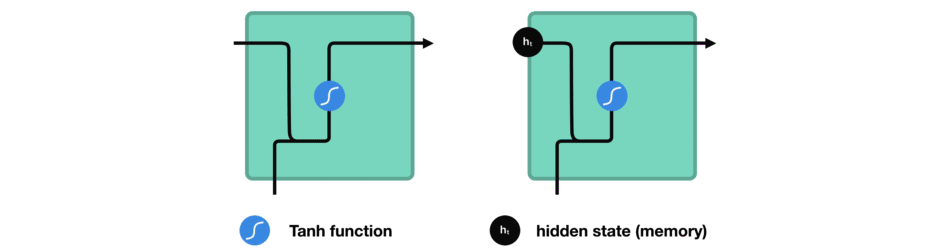
La phrase « Hier soir j’ai mangé un hamburger et des  » est convertie en vecteurs puis alimente le RNN (crédit : Michaël Nguyen)
Passage de l’état interne d’un RNN (crédit : Michaël Nguyen)

Entre chaque mot envoyé dans le RNN, la sortie, notée \(h_t\) pour le mot précédent est ajoutée en entrée avec le nouveau mot. Cette sortie est appelée l' »état caché » (hidden state en anglais)

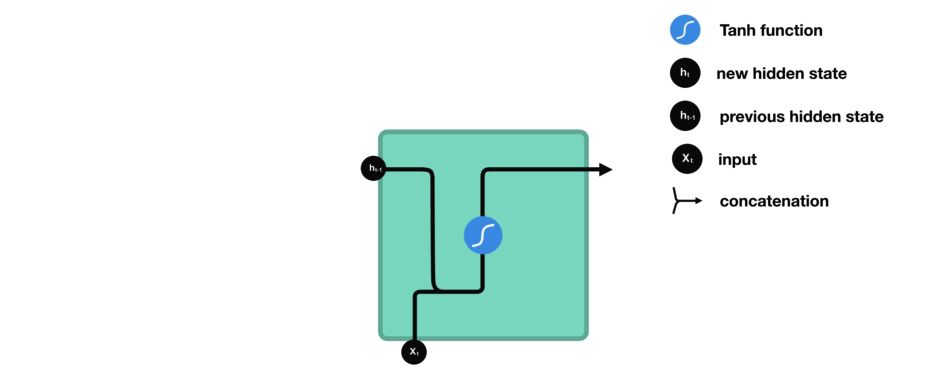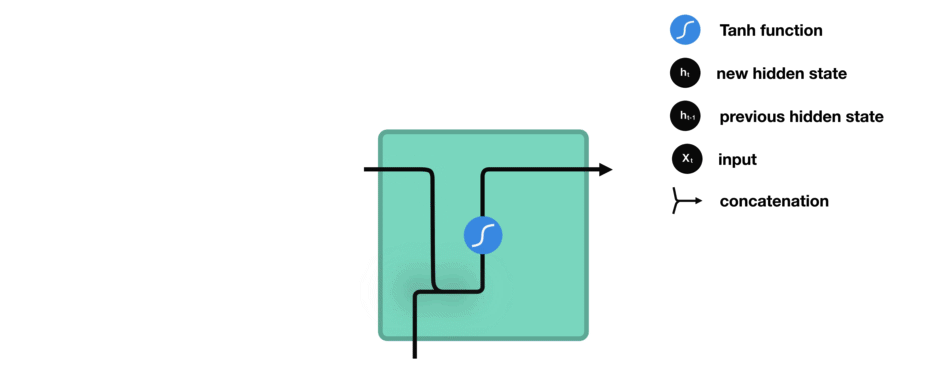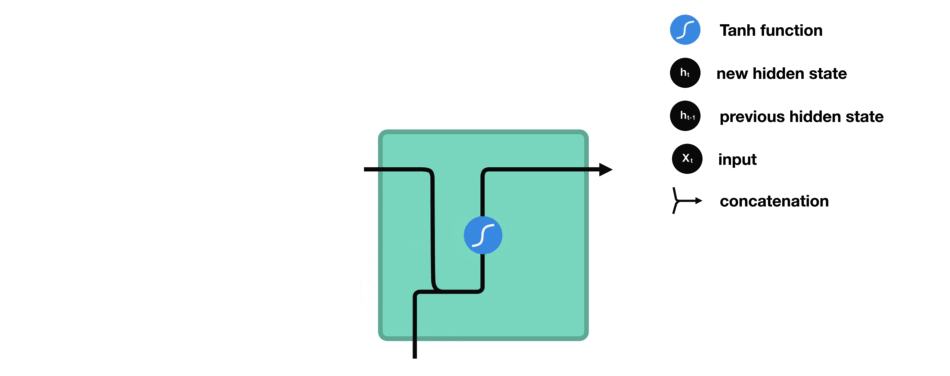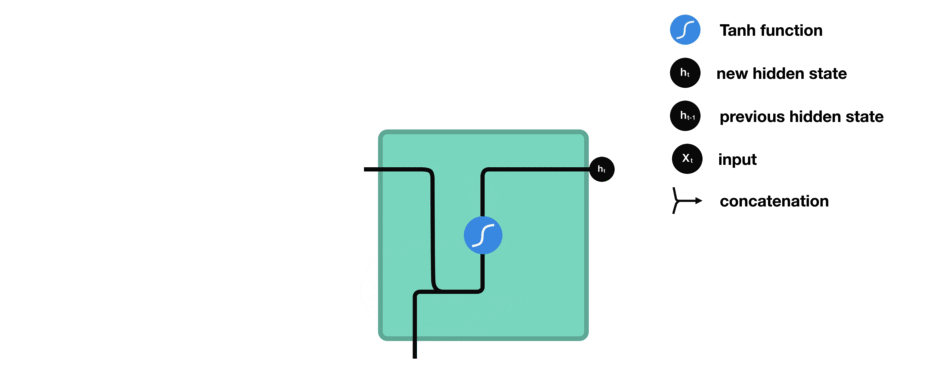
Fonctionnement interne d’un RNN (crédit : Michaël Nguyen)

Le vecteur du mot courant, noté \(x_t\), et la sortie (qui est un vecteur aussi) pour le mot précédent, notée \(h_{t-1}\), sont mises bout-à-bout puis passent dans la fonction mathématique « tanh » avant de devenir la nouvelle sortie notée \(h_t\)

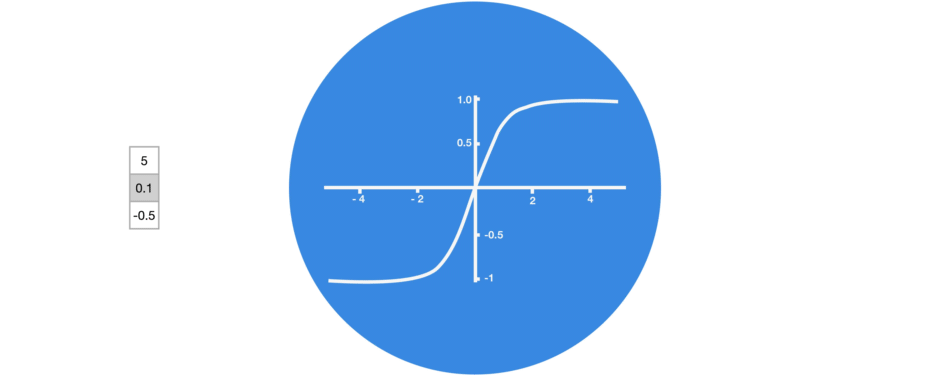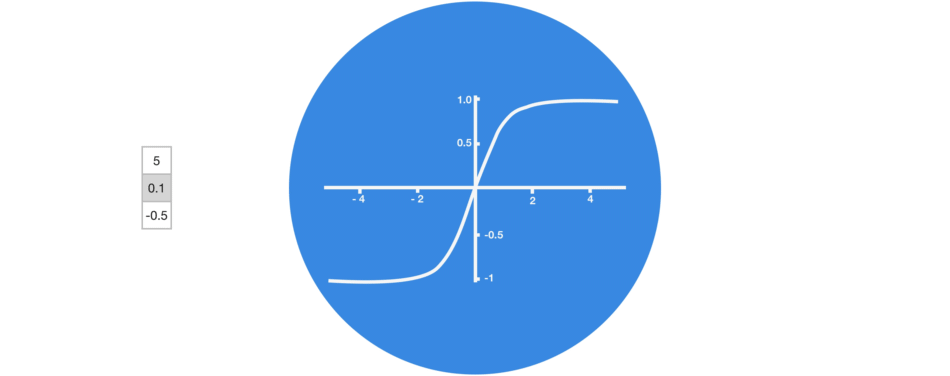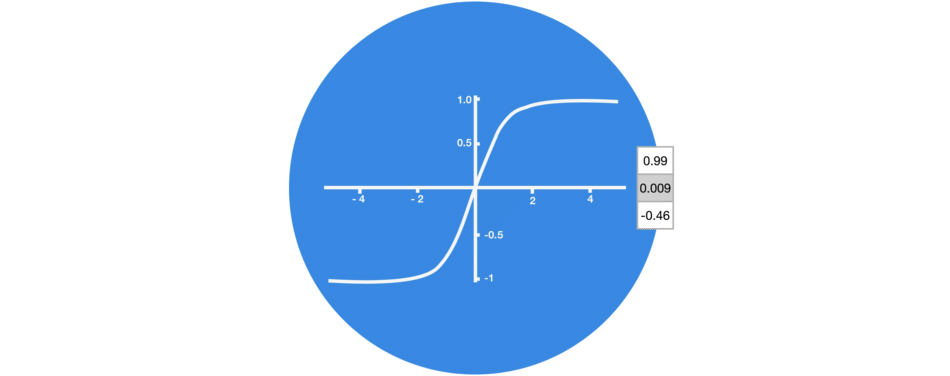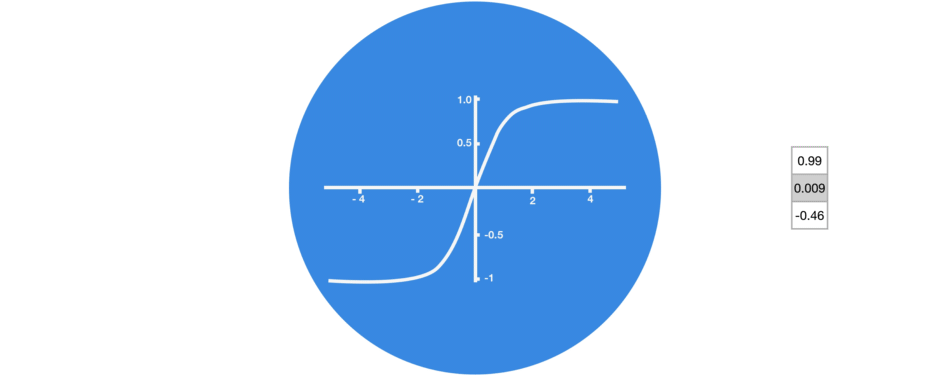
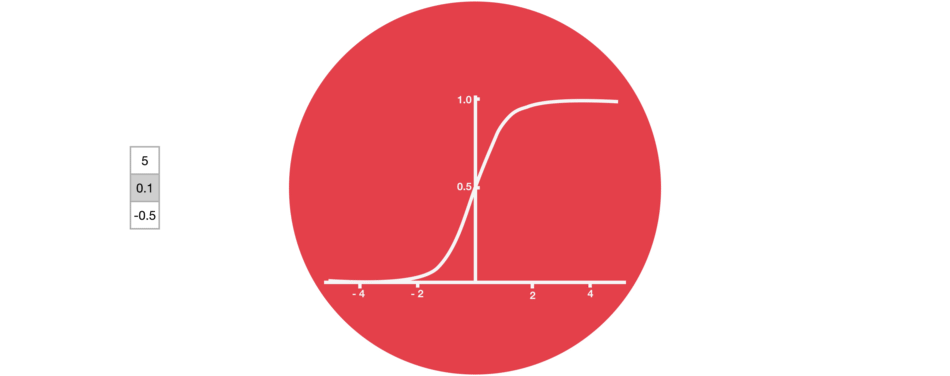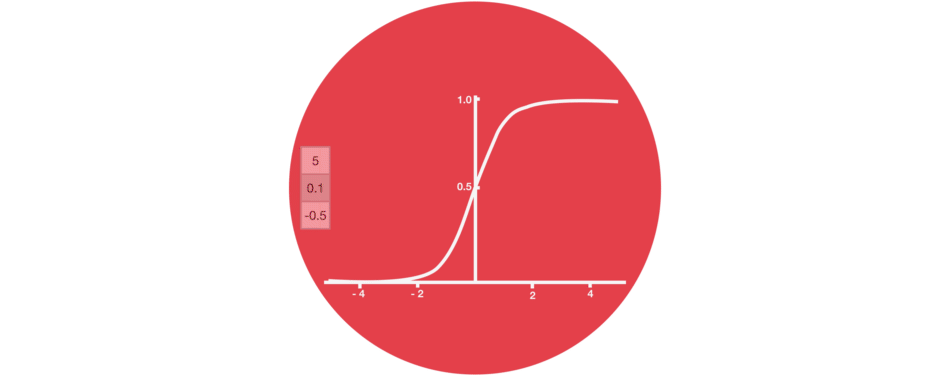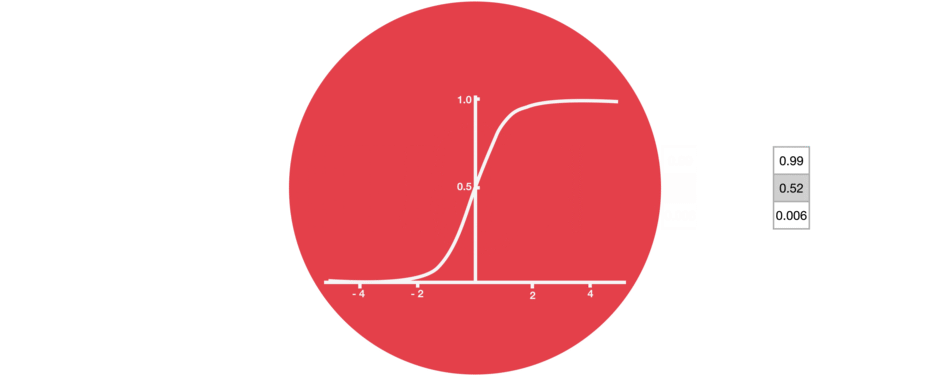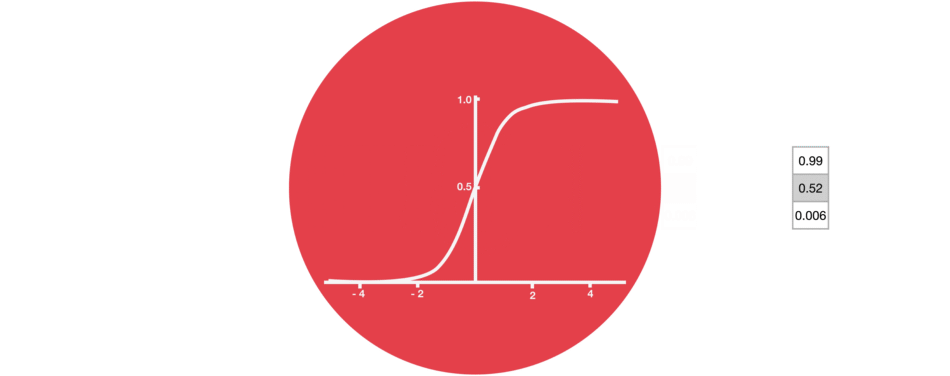
La fonction « tanh » prend une valeur en entrée et renvoie une valeur entre -1 et 1. Si on a un vecteur en entrée, alors on renvoie tanh appliquée à chaque coordonnée (crédit : Michaël Nguyen)
La fonction « sigmoid » renvoie des valeurs entre 0 et 1 (crédit : Michaël Nguyen)

Dans les réseaux de neurones, il est très fréquent d’avoir recours à des « fonctions d’activation » en sortie des neurones. Par exemple, tanh représentée ci-contre est une fonction qui convertit une valeur (par exemple 300) en une nouvelle valeur entre – 1 et 1 (cf courbe). L’intérêt d’une telle fonction est d’éviter que les sorties des neurones ne deviennent trop grandes, car cela demanderait alors plus de temps de calculs et de mémoire d’ordinateur…

Un problème d’apprentissage et de mémoire

Comme pour le perceptron en son temps, le RNN souffre du problème de dissipation du gradient. Qu’est-ce que cela signifie ?

Pour « apprendre », un RNN utilise la méthode de la descente du gradient afin de mettre à jour les poids entre ses neurones. Cela repose sur la formule suivante :

\(w := w  – \alpha \cdot F_w\)

avec :

  • \(w\) un poids du réseau
  • \(\alpha\) la vitesse d’apprentissage du réseau
  • \(F_w\) le gradient du réseau par rapport au poids \(w\)

Problème : la mise à jour des poids se fait de droite à gauche. A mesure que l’on avance vers la gauche, le produit \(\alpha \cdot F_w\) devient très petit et les poids des premières couches de neurones ne sont quasiment pas modifiés ! Ainsi, ces couches n’apprennent strictement rien…

Et par conséquent, le RNN peut facilement oublier des données un petit peu anciennes (ou des mots assez éloignés du mot courant dans un texte) lors de la phase d’apprentissage : sa mémoire est courte.

Vers une meilleure architecture : le LSTM et le GRU

Si une cellule (neurone) d’un RNN est finalement très simple (on concatène deux vecteurs puis on applique tanh dessus), ce n’est pas le cas du LSTM et du GRU au premier abord.

Les LSTM et GRU ont été créés comme méthode permettant de gérer efficacement la mémoire à court et long terme grâce à leurs systèmes de portes. S’il en existe de nombreuses variantes, les versions d’origine (présentées ici) sont encore très très largement utilisées dans les meilleurs modèles de deep learning pour le traitement automatique du langage naturel, ce qui a trait à la reconnaissance/synthèse vocale mais aussi pour la génération de texte ou l’étude de marchés…

Comment fonctionne le LSTM

LSTM, qui signifie Long Short-Term Memory, est une cellule composée de trois « portes » : ce sont des zones de calculs qui régulent le flot d’informations (en réalisant des actions spécifiques). On a également deux types de sorties (nommées états).

  • Forget gate (porte d’oubli)
  • Input gate (porte d’entrée)
  • Output gate (porte de sortie)
  • Hidden state (état caché)
  • Cell state (état de la cellule)
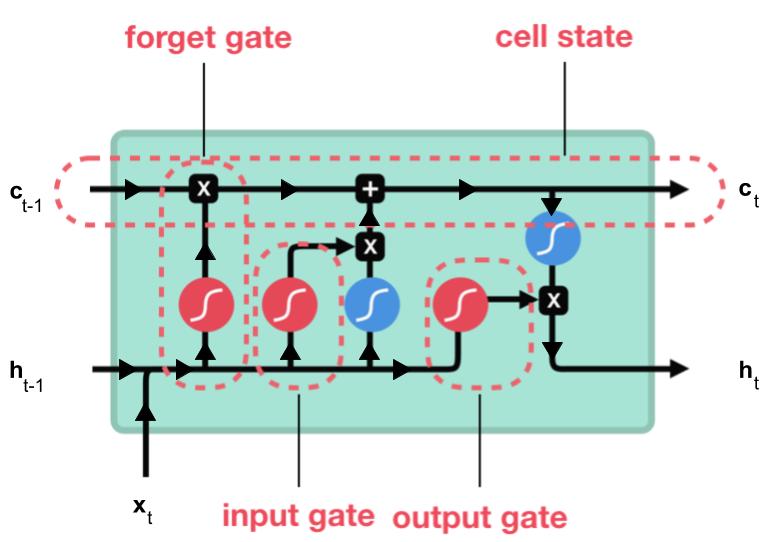
Cellule LSTM (crédit : image modifiée de Michaël Nguyen)

Commençons par comprendre toutes les opérations possibles dans un LSTM pour ne pas buter dessus ensuite.

Opérations internes que l’on retrouve dans le LSTM (crédit : Lambert Rosique avec les icônes des images de Michaël Nguyen)

Ces opérations dans les portes permettent au LSTM de conserver ou supprimer des informations qu’il a en mémoire. Par exemple, dans notre phrase « Hier soir j’ai mangé un hamburger et des », il est important de retenir les mots « hamburger » et « manger » tandis que les déterminants « un », « et » peuvent être oubliés par le réseau.

Les données stockées dans la mémoire du réseau sont en fait un vecteur noté \(c_t\) : l’état de la cellule. Comme cet état dépend de l’état précédent \(c_{t-1}\), qui lui-même dépend d’états encore précédents, le réseau peut conserver des informations qu’il a vu longtemps auparavant (contrairement au RNN classique).

Comment fait le réseau LSTM pour apprendre, quelles sont ses variables internes ?

Les entrées de chaque porte sont pondérées par des poids liés aux portes ainsi que par un biais. On a 4 matrices de poids (leurs dimensions dépendent des dimensions de \(h_{t-1}\) et \(x_t\)) :

  • \(W_f\) : pondère l’entrée de la porte d’oubli (forget gate)
  • \(W_i\) : pondère l’entrée de la porte d’entrée (input gate)
  • \(W_C\) : pondère les données qui vont se combiner à la porte d’entrée pour mettre à jour l’état de la cellule (cell state)
  • \(W_o\) : pondère l’entrée de la porte de sortie (output gate)
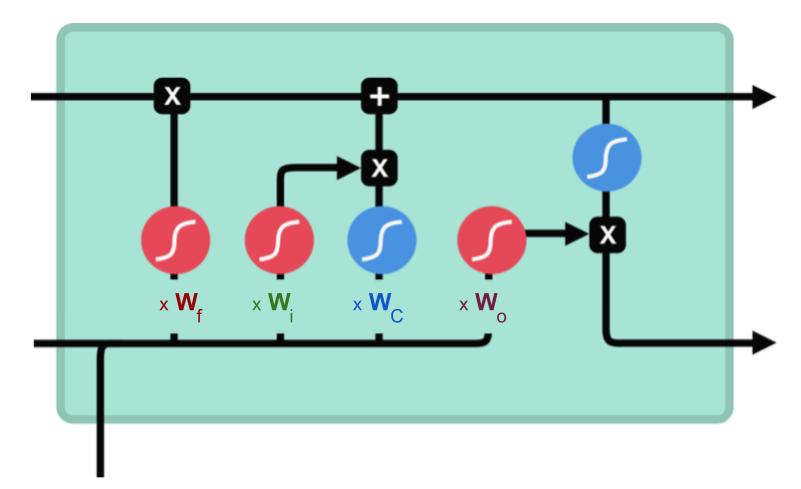
Le LSTM dispose de « 4 matrices de poids » (avec leurs biais) contrôlant ses portes (crédit : image modifiée de Michaël Nguyen)

Détaillons à présent ce que fait chaque porte, en gardant en mémoire que les données sont pondérées par les poids W (auxquels on ajoute un biais qui dépend de la porte et qui est aussi mis à jour dans la phase d’apprentissage).

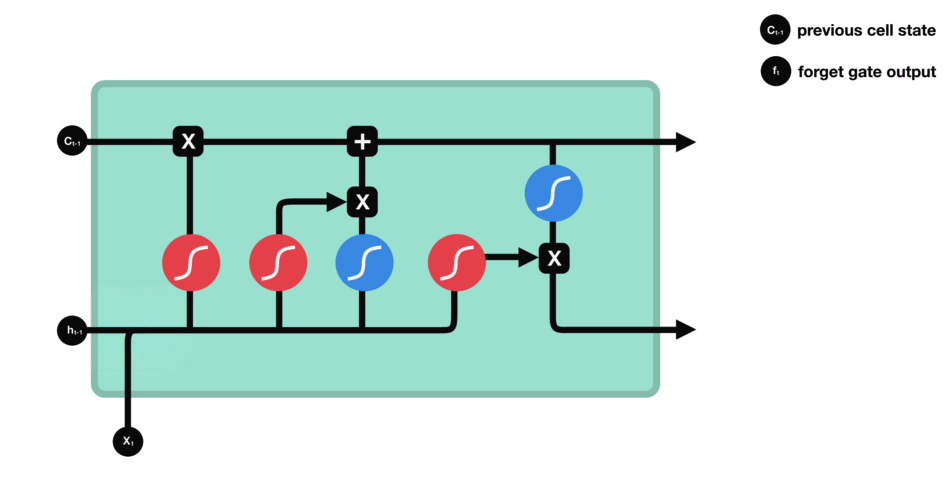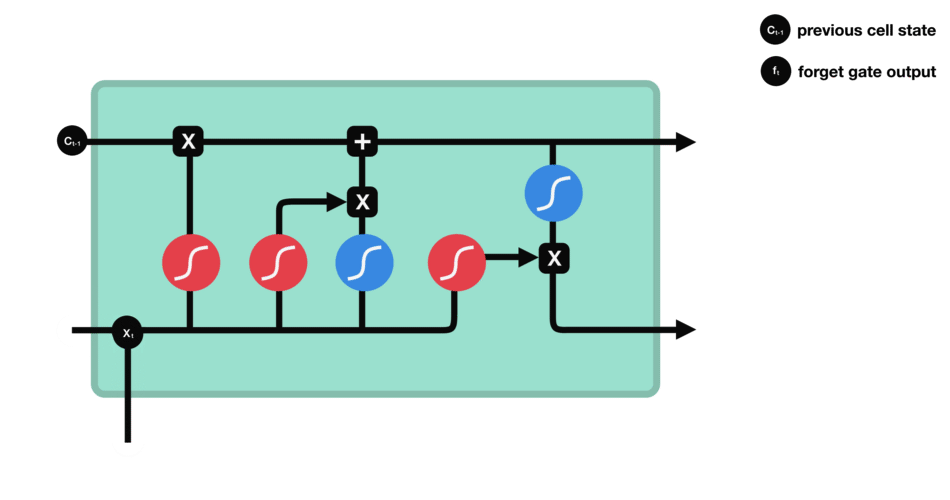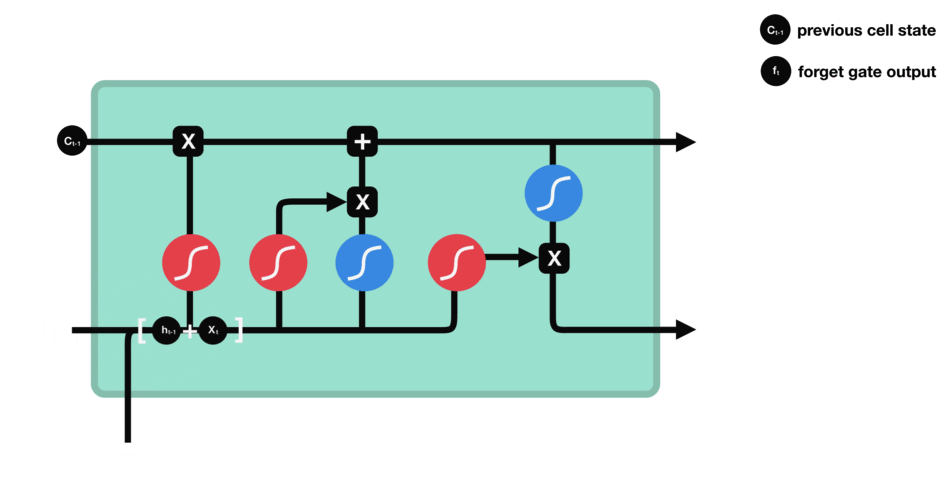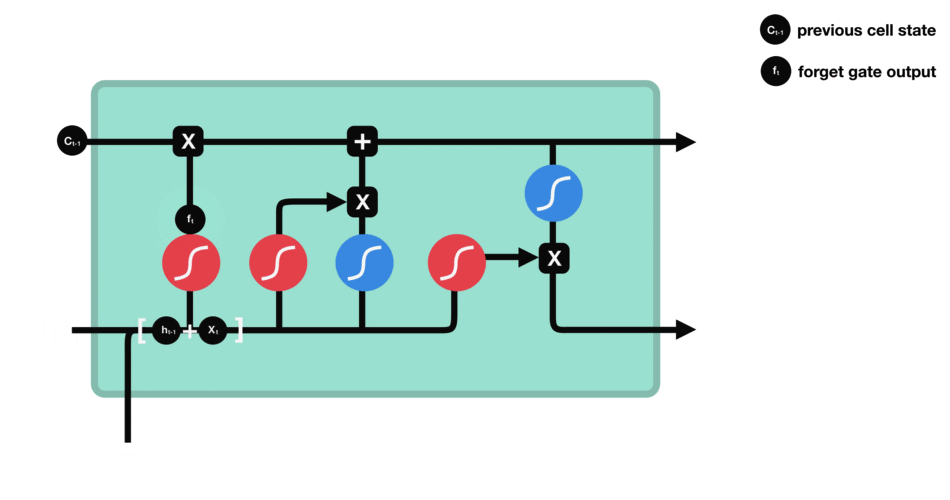
Porte d’oubli (forget gate)

Cette porte décide de quelle information doit être conservée ou jetée : l’information de l’état caché précédent est concaténé à la donnée en entrée (par exemple le mot « des » vectorisé) puis on y applique la fonction sigmoïde afin de normaliser les valeurs entre 0 et 1. Si la sortie de la sigmoïde est proche de 0, cela signifie que l’on doit oublier l’information et si on est proche de 1 alors il faut la mémoriser pour la suite.

Fonctionnement de la porte d’oubli d’un LSTM (crédit : Michaël Nguyen)

Porte d’entrée (input gate)

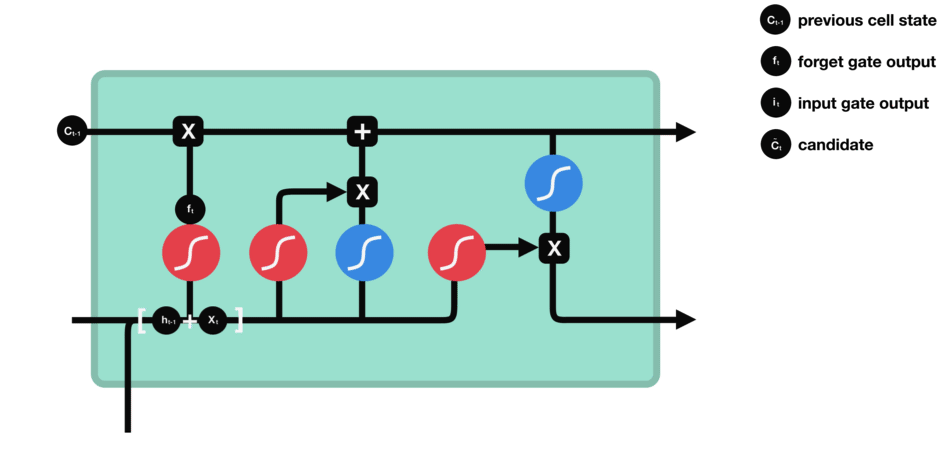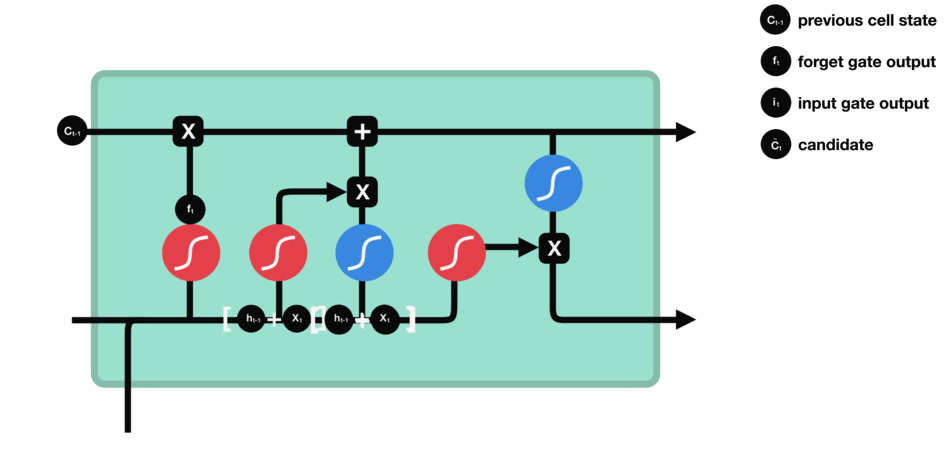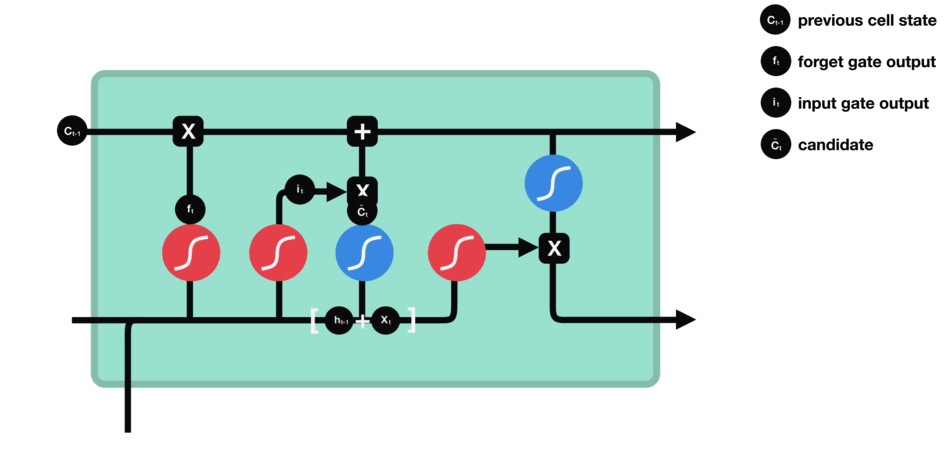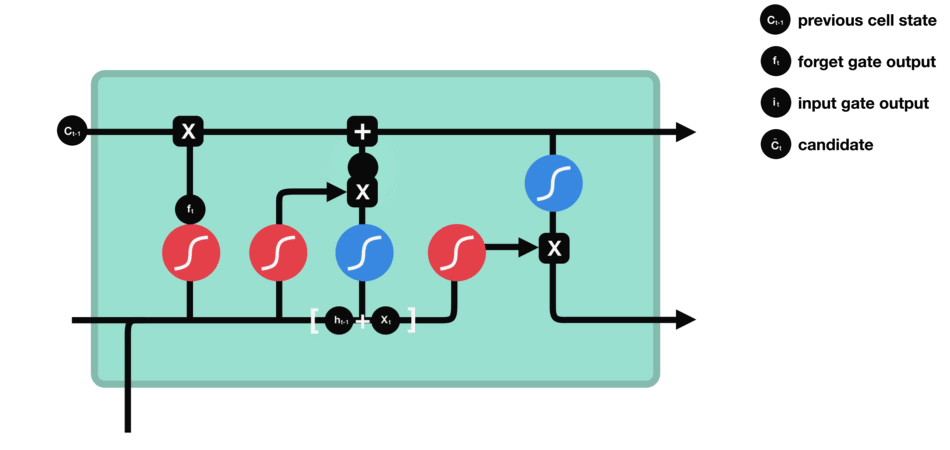
La porte d’entrée a pour rôle d’extraire l’information de la donnée courante (le mot « des » par exemple) : on va appliquer en parallèle une sigmoïde aux deux données concaténées (cf porte précédente) et une tanh.

  • Sigmoïde va renvoyer un vecteur pour lequel une coordonnée proche de 0 signifie que la coordonnée en position équivalente dans le vecteur concaténé n’est pas importante. A l’inverse, une coordonnée proche de 1 sera jugée « importante » (i.e. utile pour la prédiction que cherche à faire le LSTM).
  • Tanh va simplement normaliser les valeurs (les écraser) entre -1 et 1 pour éviter les problèmes de surcharge de l’ordinateur en calculs.
  • Le produit des deux permettra donc de ne garder que les informations importantes, les autres étant quasiment remplacées par 0
Fonctionnement de la porte d’entrée d’un LSTM (crédit : Michaël Nguyen)

Etat de la cellule (cell state)

On parle de l’état de la cellule avant d’aborder la dernière porte (porte de sortie), car la valeur calculée ici est utilisée dedans.

L’état de la cellule se calcule assez simplement à partir de la porte d’oubli et de la porte d’entrée : d’abord on multiplie coordonnée à coordonnée la sortie de l’oubli avec l’ancien état de la cellule. Cela permet d’oublier certaines informations de l’état précédent qui ne servent pas pour la nouvelle prédiction à faire. Ensuite, on additionne le tout (coordonnée à coordonnée) avec la sortie de la porte d’entrée, ce qui permet d’enregistrer dans l’état de la cellule ce que le LSTM (parmi les entrées et l’état caché précédent) a jugé pertinent.

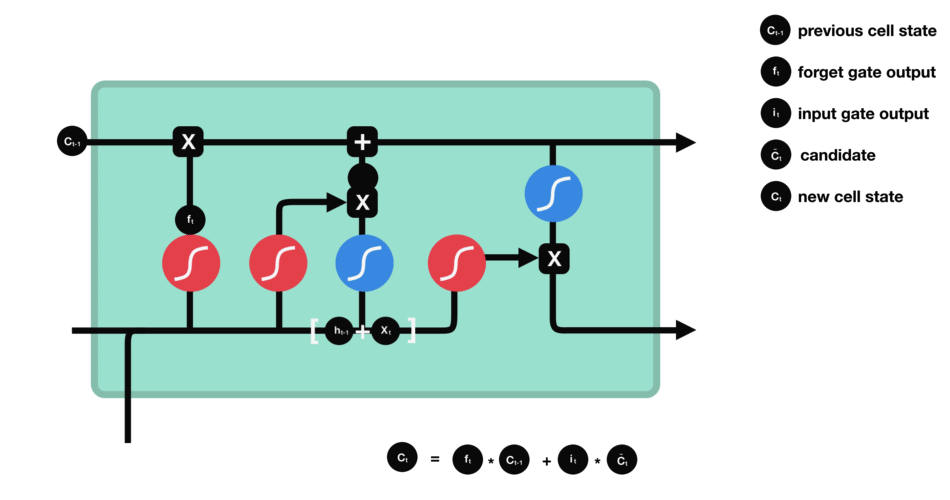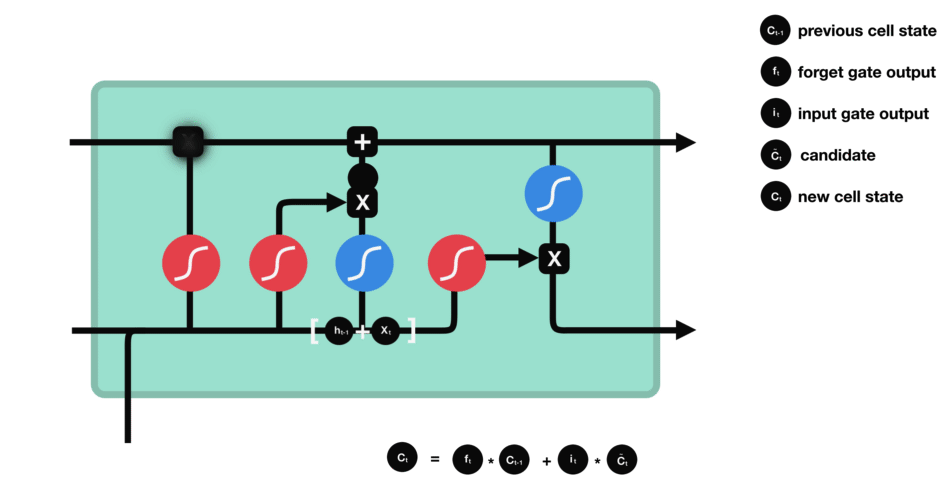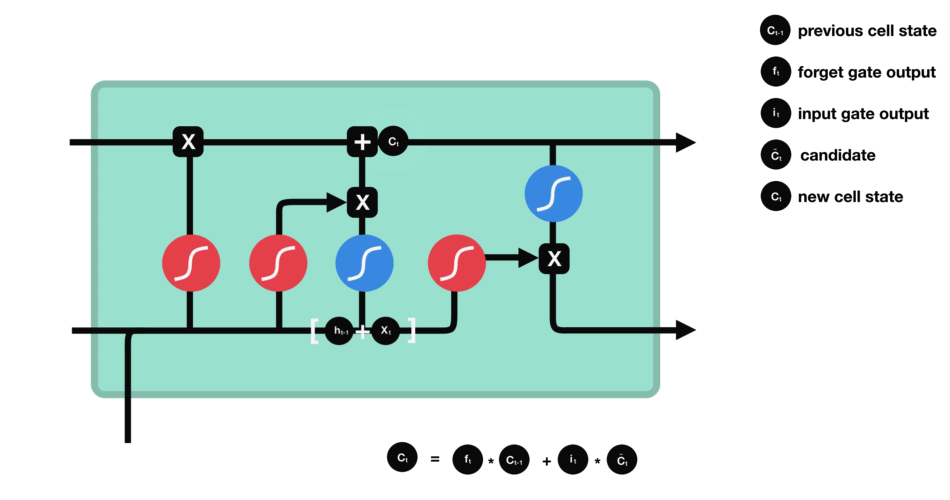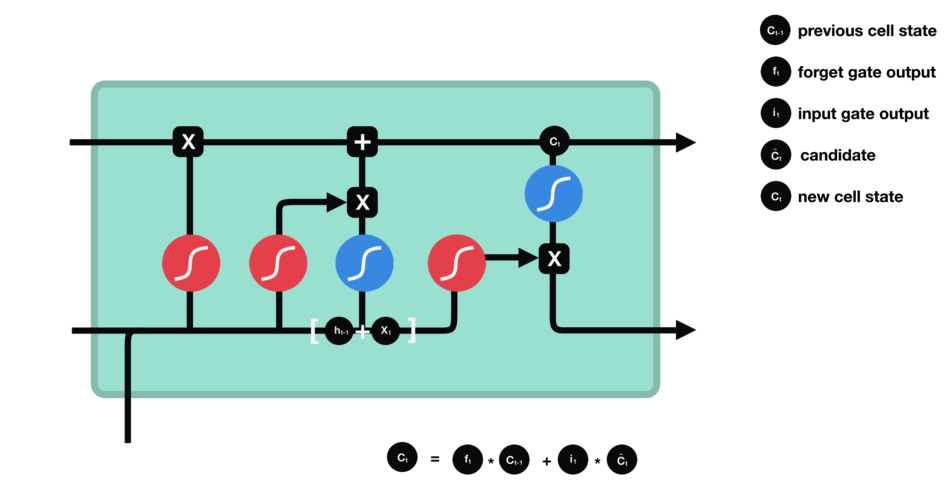
Mise à jour de l’état de la cellule d’un LSTM (crédit : Michaël Nguyen)

Porte de sortie (output gate)

Dernière étape : la porte de sortie doit décider de quel sera le prochain état caché, qui contient des informations sur les entrées précédentes du réseau et sert aux prédictions.

Pour ce faire, le nouvel état de la cellule calculé juste avant est normalisé entre -1 et 1 grâce à tanh. Le vecteur concaténé de l’entrée courante avec l’état caché précédent passe, pour sa part, dans une fonction sigmoïde dont le but est de décider des informations à conserver (proche de 0 signifie que l’on oublie, et proche de 1 que l’on va conserver cette coordonnée de l’état de la cellule).

Tout cela peut sembler magique en ce sens où on dirait que le réseau doit deviner ce qu’il doit retenir dans un vecteur à la volée, mais rappelons bien qu’une matrice de poids est appliquée en entrée. C’est cette matrice qui va, concrètement, stocker le fait que telle information est importante ou non à partir des milliers d’exemples qu’aura vu le réseau !

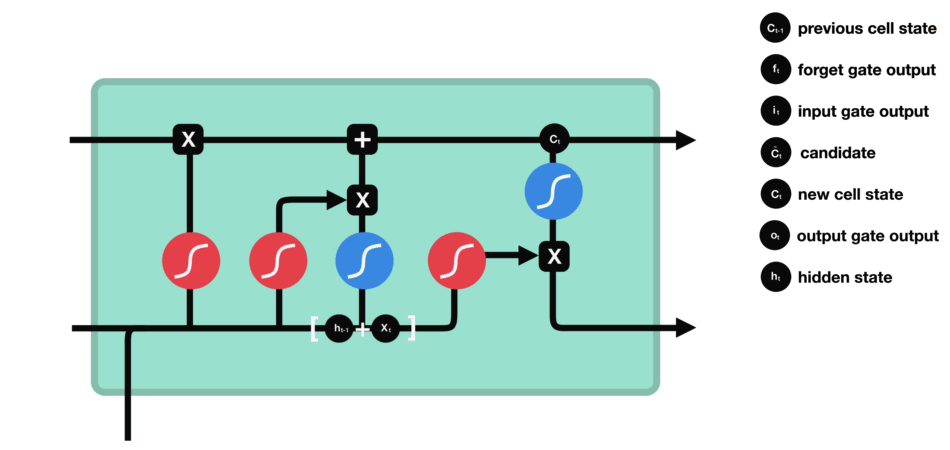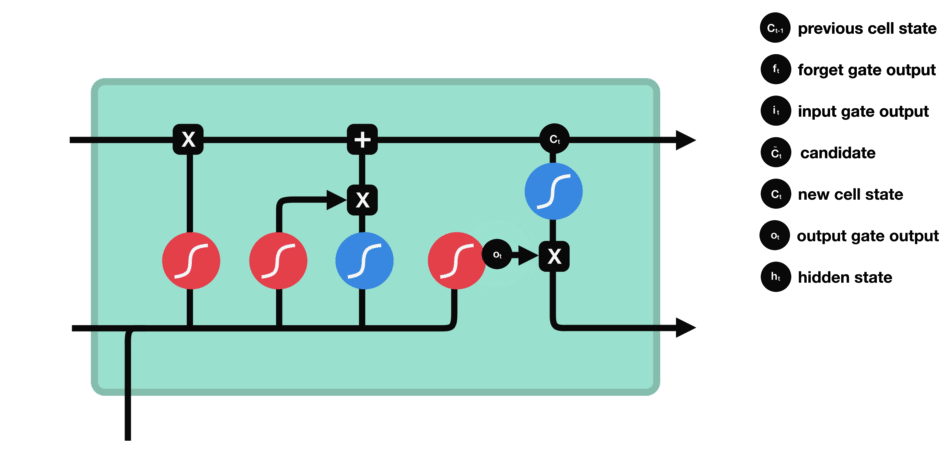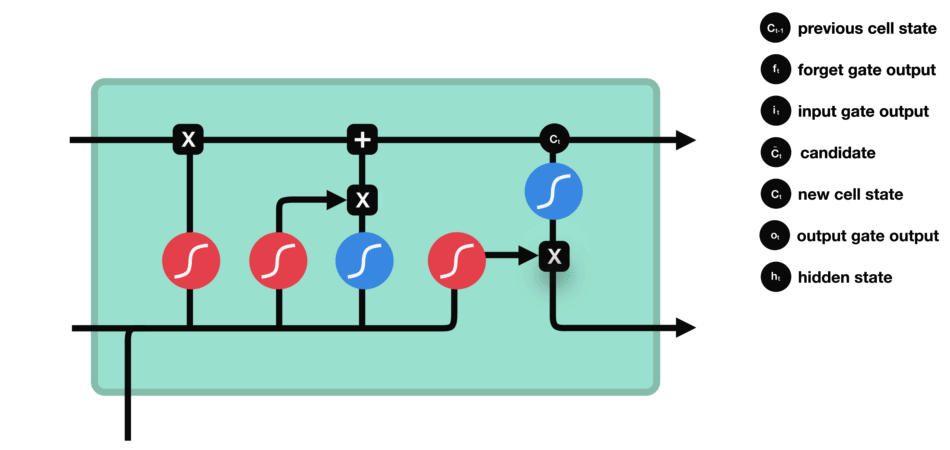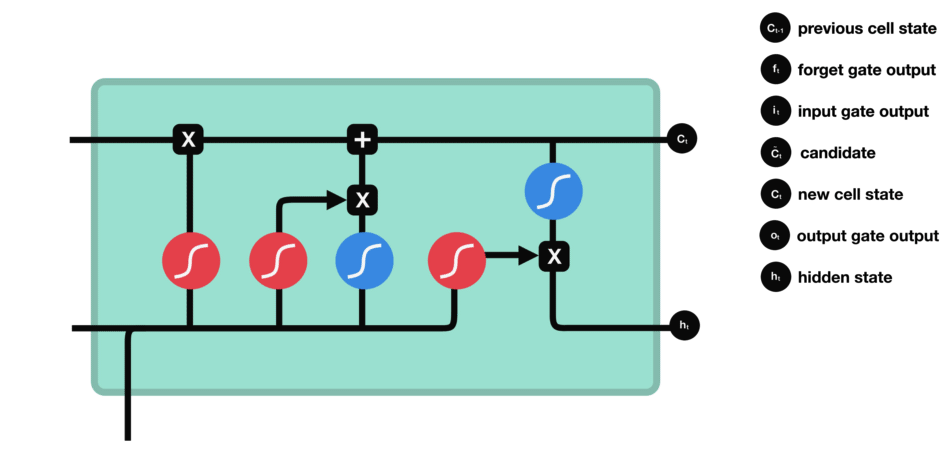
Fonctionnement de la porte de sortie d’un LSTM (crédit : Michaël Nguyen)

Comment fonctionne le GRU

GRU, Gated Recurrent Unit, pour sa part dispose de deux portes et un état en sortie :

  • Reset gate (porte de reset)
  • Update gate (porte de mise à jour)
  • Cell state (état de la cellule)
Cellule GRU (crédit : Michaël Nguyen)

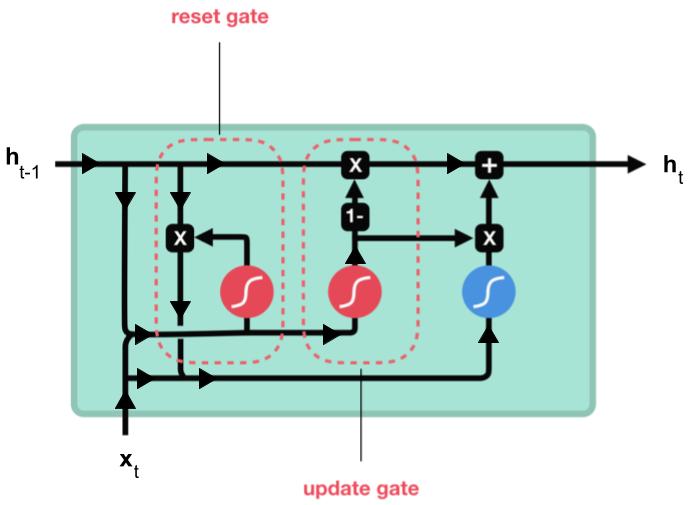
Voici les différentes fonctions que l’on va trouver dans la cellule.

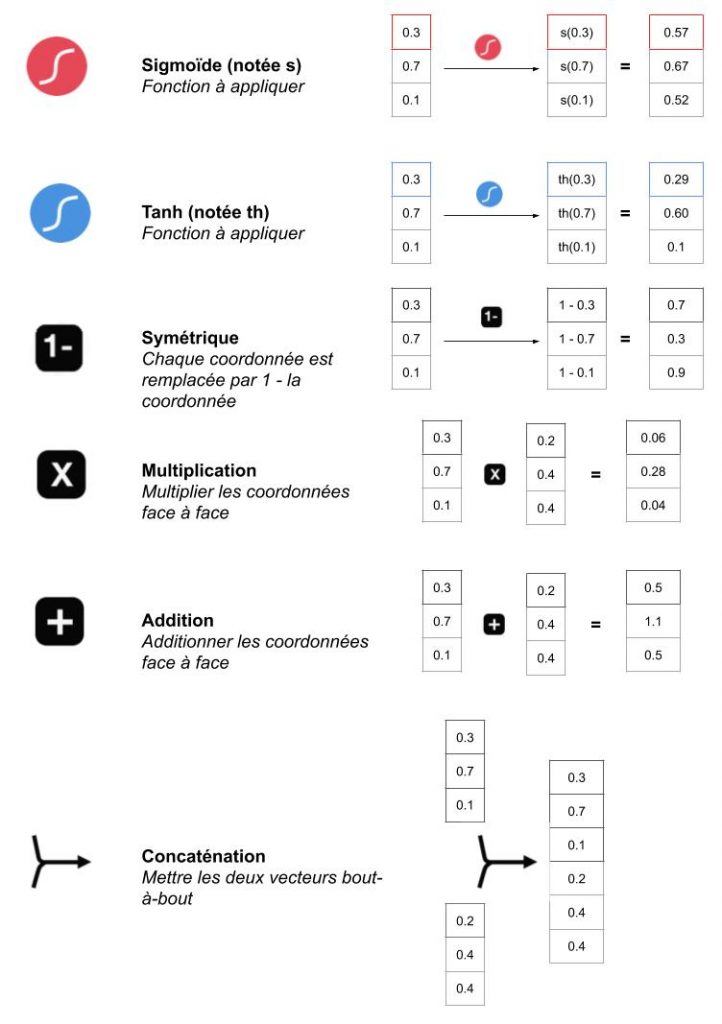
Opérations dans un GRU. La seule différence avec le LSTM est « 1 – » (crédit : Lambert Rosique à partir des icônes des images de Michaël Nguyen)

Une fois que l’on a compris le fonctionnement du LSTM, celui du GRU n’est pas très éloigné (quoique plus simple). A noter l’apparition d’une nouvelle opération qui consiste à inverser un vecteur par rapport à 1 (on calcule 1 – le vecteur). Ceci a pour objectif d’inverser les conclusions d’une porte (par exemple, que tout ce qui a été jugé important devienne anodin et vice versa) : en logique, c’est une porte NOT.

Mais tout d’abord… qu’apprend le GRU ?

Voici un schéma de l’emplacement des matrices de poids qui viennent pondérer les vecteurs entrant dans les portes.

  • \(W_r\) : pondère l’entrée de la porte de reset (reset gate)
  • \(W_z\) : pondère l’entrée de la porte de mise à jour (update gate)
  • \(W_h\) : pondère les données qui vont se combiner pour définir l’état caché courant
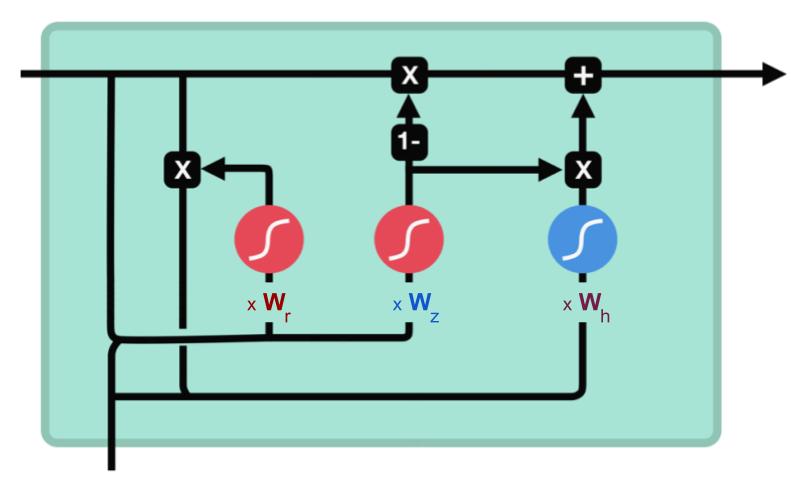
Le GRU dispose de « 3 matrices de poids » (avec leurs biais) contrôlant ses portes (crédit : image modifiée de Michaël Nguyen)

Porte de reset (reset gate)

Cette porte sert à contrôler combien d’information passée le réseau doit oublier. L’état caché précédent, concaténé avec les données d’entrée, passe par une sigmoïde (pour ne conserver que les coordonnées pertinentes) puis est multiplié par l’ancien état caché : on n’en conserve donc que les coordonnées importantes (telles qu’elles) de l’état précédent (on a donc perdu une partie de l’état précédent dans cette porte).

Porte de mise à jour (update gate)

Cette porte agit exactement de la même manière que les portes oubli et d’entrée du LSTM : elle décide des informations à conserver et de celles à oublier.

Les données d’entrées et l’ancien état caché sont concaténés et passent par une fonction sigmoïde dont le rôle est de déterminer quelles sont les composantes importantes.

Sortie du réseau GRU

L’état caché précédent (partiellement effacé par la porte de reset) est combiné avec l’entrée du réseau et normalisé par un tanh entre -1 et 1. On vient ensuite annuler toutes ses coordonnées jugées « inutiles pour les prédictions » (grâce à la sortie de la porte de mise à jour), puis on y ajoute les coordonnées de l’état caché précédent jugées « inutiles » (en ayant, cette fois, annulé toutes les coordonnées pertinentes).

Les calculs opérés par le GRU sont plus rapides et plus simples. Notons cependant que les capacités/l’efficacité de ce dernier ne sont plus à prouver, et il est autant utilisé que le LSTM.

Remerciements

Je voulais remercier Michaël Nguyen pour son excellent travail de présentation sur Medium (en anglais) des LSTM et GRU, et en particulier pour les schémas repris ici qu’il m’a autorisé à utiliser (avec la traduction de son article) !

En écrivant/traduisant cet article j’ai non seulement fini par comprendre (fondamentalement) comment marchent les deux types de cellules LSTM et GRU, mais j’ai aussi appris à faire de beaux schémas animés ^^

N’hésitez pas à regarder la vidéo de Michaël :

Crédit de l’image de couverture : Michaël Nguyen

ARTICLES CONNEXESPLUS DE L'AUTEUR