L’analyse en composantes principales (PCA) est un algorithme de machine learning non supervisé mis en place lorsque le nombre de dimensions est très grand.
Sa catégorisation dans les algorithmes non supervisés, signifie que son apprentissage s’effectue sur un jeu de données non étiquetées. Afin de mieux comprendre la notion d’étiquetage, considérons, par exemple, que l’objectif d’une étude est de déterminer si les caractéristiques d’un individu entraînent l’apparition d’une maladie. Chaque patient possède un certain nombre de caractéristiques mais il a également une étiquette correspondant à « malade » ou « non malade ». Ainsi, lorsque l’on dit que l’apprentissage est réalisé sur des données non étiquetées, cela signifie que l’apprentissage est exclusivement effectué à partir des caractéristiques des individus.
Introduction à l’analyse en composantes principales
La PCA permet de simplifier nos données en faisant ressortir les caractéristiques les plus pertinentes. En d’autres termes, il permet de réduire les dimensionnalités des jeux de données tout en préservant autant de variabilités que possible.
Pour mieux comprendre, voici un exemple. En parlant à des amis, vous décidez de nommer la personne de votre classe que vous avez rencontrée ce matin. Cependant vous n’avez plus son nom. Vous choisissez de la décrire car chaque camarade de classe possède de très nombreuses caractéristiques comme son tempérament, son âge, sa taille, etc. Cependant l’énumération de l’ensemble de ses caractéristiques serait laborieux et non pertinent. En effet, beaucoup d’entre elles mesureront les propriétés associées et seront donc redondantes. Si tel est le cas, nous devrions pouvoir résumer chaque camarade avec moins de caractéristiques. Attention cependant, la PCA ne sélectionne pas certaines caractéristiques et rejette les autres. Au lieu de cela, elle construit de nouvelles caractéristiques qui permettent de mieux séparer nos camarades. Bien sûr, ces nouvelles caractéristiques sont construites en utilisant les anciennes. Par exemple, une nouvelle caractéristique comme la prestance peut être calculée à partir de la taille et de la largeur d’un individu. En fait, la PCA trouve les meilleures caractéristiques possibles, celles qui résument au mieux la liste de nos camarade.
La première mention de cet algorithme apparaît dans une publication de Pearson K. de 1901 « On lines and planes of closest fit to systems of points in space. Phil. Mag. 2, 559–572 ». Cependant, ce n’est que des années plus tard, suite à la démocratisation des outils informatiques qu’il sera appliqué pour le traitement d’importantes quantités de données.
Dans cet article, il s’agit dans un premier temps de vous expliquer les problèmes auxquels sont confrontés les scientifiques lorsque le nombre de dimension devient trop grand. Puis de vous présenter via deux types d’approches, géométrique et numérique ,l’analyse en composantes principales comme un outil de réduction de la dimensionalité . Dans un second article, nous aborderons les limites principales de cet algorithme. Et nous verrons que les scientifiques ont su faire preuve d’ingéniosité afin de contourner ses limites et de s’adapter à des données de plus en plus variées.
Malédiction de la dimensionnalité
Un grand nombre de dimensions entraîne trois problèmes principaux. Premièrement la visualisation des données devient beaucoup plus complexe lorsque l’on a un espace de plus de trois dimensions. Le deuxième inconvénient, lorsque le nombre de dimensions devient très important, repose sur la limite de puissance de calcul d’un ordinateur. En effet, l’augmentation du nombre de dimensions entraîne une augmentation du nombre de calculs à effectuer, ce qui a pour conséquence une augmentation du temps de calcul. La dernière difficulté à laquelle nous sommes confrontés est la sur-interprétation. Ce phénomène se produit lorsque l’algorithme colle parfaitement aux données sur lequel il a été entraîné, mais ne se généralise pas à d’autres données. Cela signifie que l’algorithme ne prend pas en considération les variations liées au hasard et aux biais lors de la sélection des données.
Pour se lancer face à des espaces de si grande dimension, les scientifiques ont dans leurs sacs de très nombreux outils, dont la fameuse analyse en composantes principales (PCA). Cet algorithme se base sur l’identification de la direction de plus grandes variations d’un ensemble de données, grâce à l’analyse des covariances. Cette direction est appelée la composante principale.
Matrice de covariance
Du point de vue mathématique, cet algorithme utilise un outil appelé la matrice de covariance, indiqué par la lettre grecque « Sigma » de symbole Σ.
Cette matrice est un tableau carré composé de P lignes et de P colonnes. On dit que la matrice est de dimension « P*P ». On considère P comme le nombre de dimensions initiales. En fait, si chaque individu possède 200 caractéristiques alors P sera égal à 200.
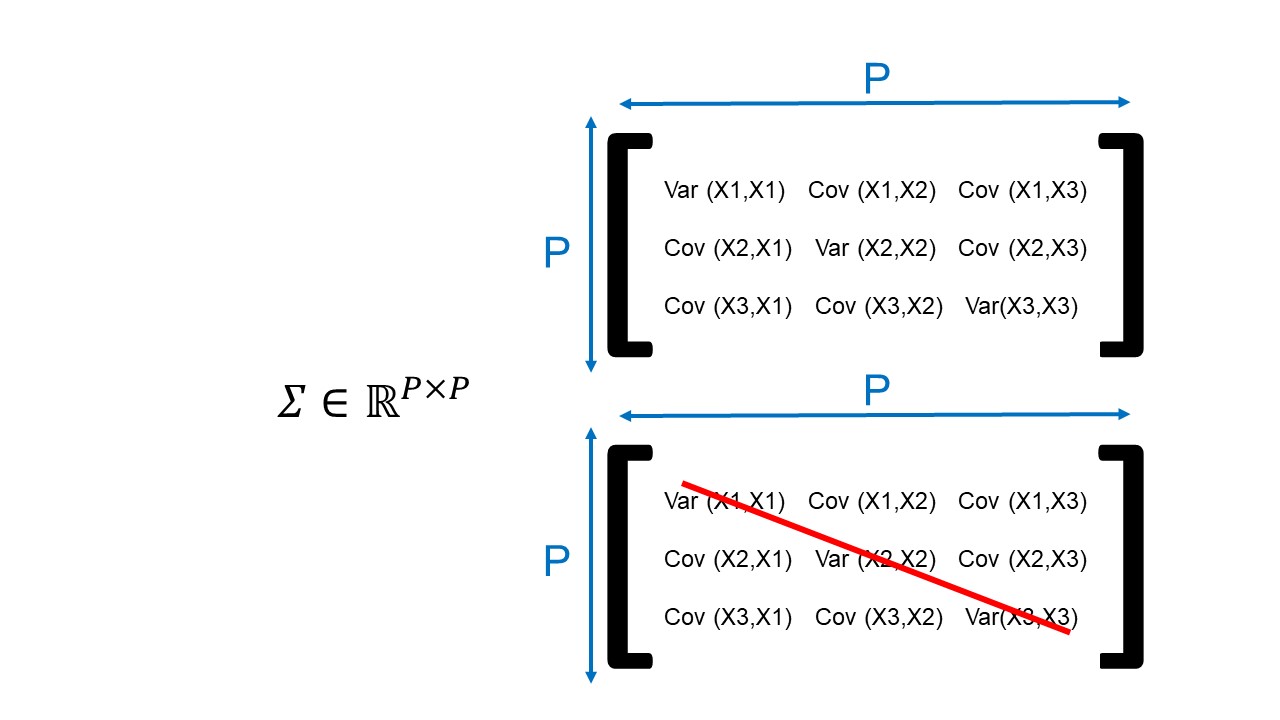
Plus précisément, cette matrice de covariance contient en diagonale les variances et en extra-diagonale les covariances; on dit que la matrice de covariance est symétrique (Figure 1). Par exemple, la valeur de coordonnée (première ligne, première colonne) correspond à la variance de la première dimension (Var(X1,X1), Figure 1). La valeur de coordonnée (première ligne, deuxième colonne) correspond à la variance entre la première dimension et la seconde dimension. Pour cette dernière, comme les dimensions comparées ne sont pas identiques, la variance est appelée covariance (Cov(X1,X2), Figure 1).
En somme, nous pouvons dire que la matrice de covariance permet de savoir comment la iième (ith en anglais) coordonnée de la matrice varie avec à la jième (jth en anglais) coordonnée de la matrice (Σij = Cov(ith coordonnée, jth coordonnée)).
Variance et Covariance
Par définition, le terme de variance correspond au nombre qui permet de quantifier la dispersion des valeurs d’un échantillon. En particulier, elle permet de mesurer les écarts conjoints des variables par rapport à leurs moyennes respectives. La formulation arithmétique nous dit que la variance est égale à la différence entre la moyenne des carrés et le carré de la moyenne (Figure 2A). Attention, il ne faut pas confondre la variance et l’écart type d’un échantillon. L’écart type correspond à la racine carrée de la variance.
En revanche, la covariance notée « Cov » est une extension de la notion de variance notée « Var ». Elle correspond aux variations simultanées de deux variables aléatoires (Figure 2B).
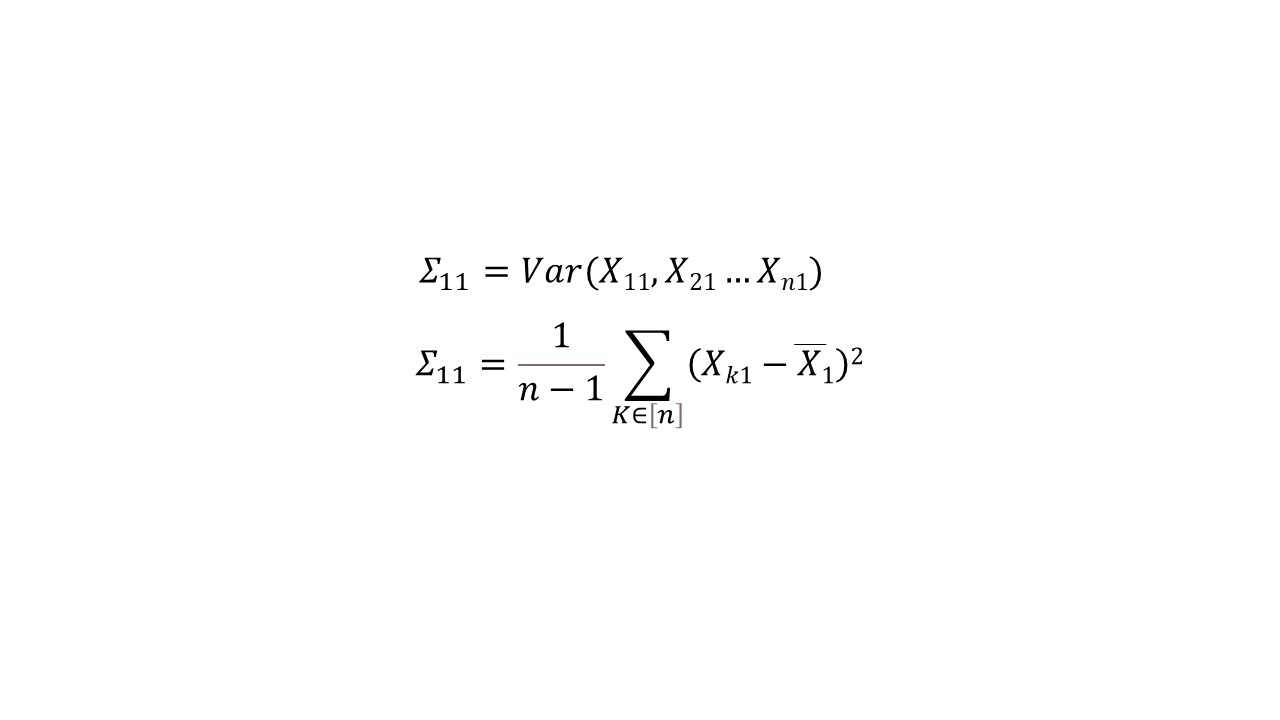
A : Formulation arithmétique de la variance de sigma pour les coordonnées 1,1. 
B : Formulation arithmétique plus détaillée de la matrice de covariance.
Approche géométrique de l’analyse en composantes principales
L’utilisation d’un graphique est une solution intuitive pour comprendre comment fonctionne cet algorithme. Ce type d’approche peut être décomposé en 3 étapes : Le centrage des données par rapport à l’origine, la détermination des composantes principales et enfin la hiérarchisation des composantes principales.
Centrer nos données par rapport à l’origine
La première étape de l’analyse en composantes principales consiste à placer nos données sur le graphe (Figures 3A & B). Pour faire ceci nous plaçons l’échantillon 1. Ces coordonnées sont X11 sur la dimension 1, X12 sur la dimension 2, etc. Chaque caractéristique peut être vue comme une dimension. Ensuite, on réalise cette étape pour l’échantillon 2 puis l’échantillon 3 et enfin l’échantillon 4. Une fois l’ensemble de nos données placées, la moyenne de chaque caractéristique est calculée (Figure 3C).
L’intersection de ces moyennes est placée à l’origine (Figure 3D). Cette étape permet de centrer nos données par rapport à l’origine en préservant les variations de nos données les unes par rapport aux autres.
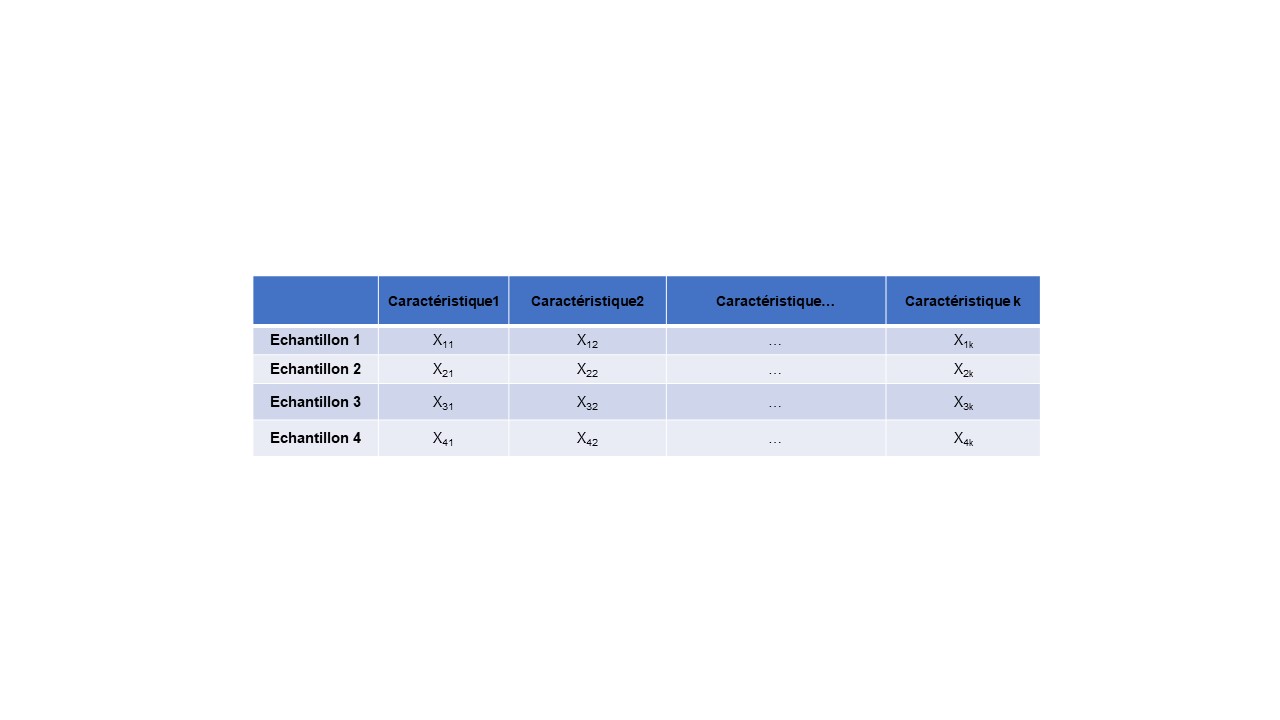
A : Données. 
B : Etape 1 – placer les données sur le graphe. 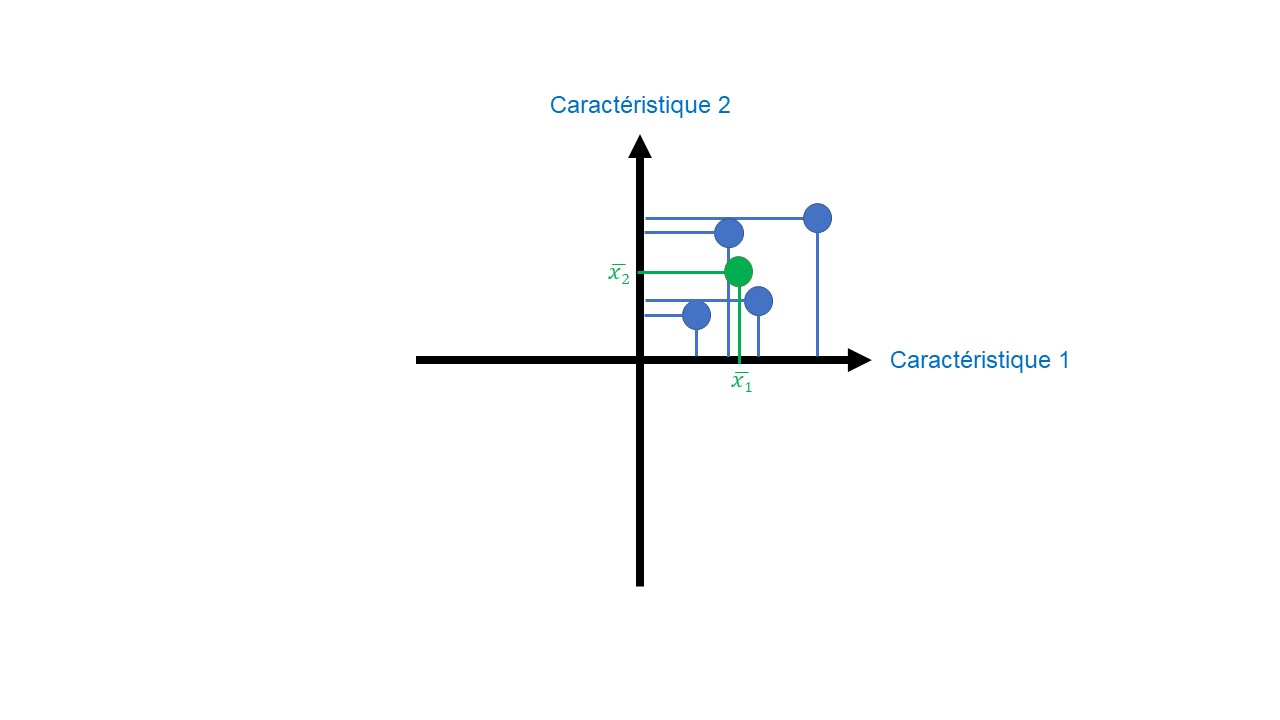
C : Etape 2 – calculer les moyennes. 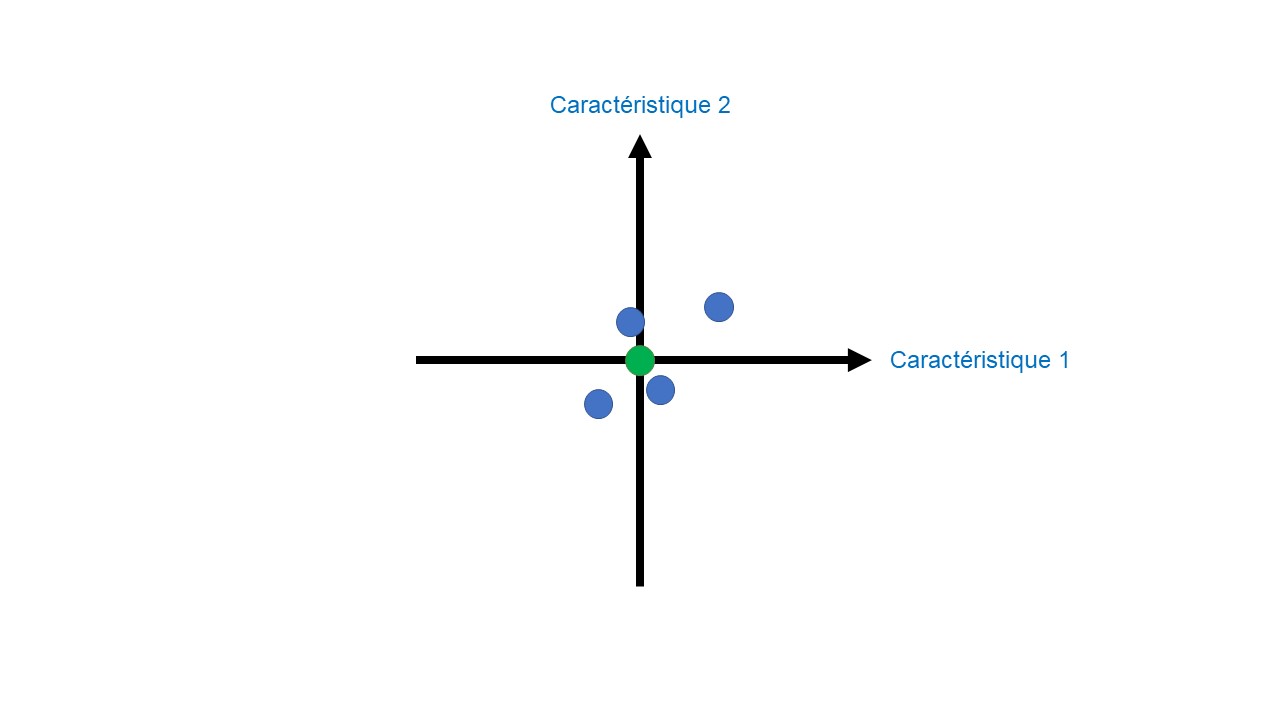
D : Etape 3 – centrer les données.
Composantes principales dans une base orthonormée et valeurs propres
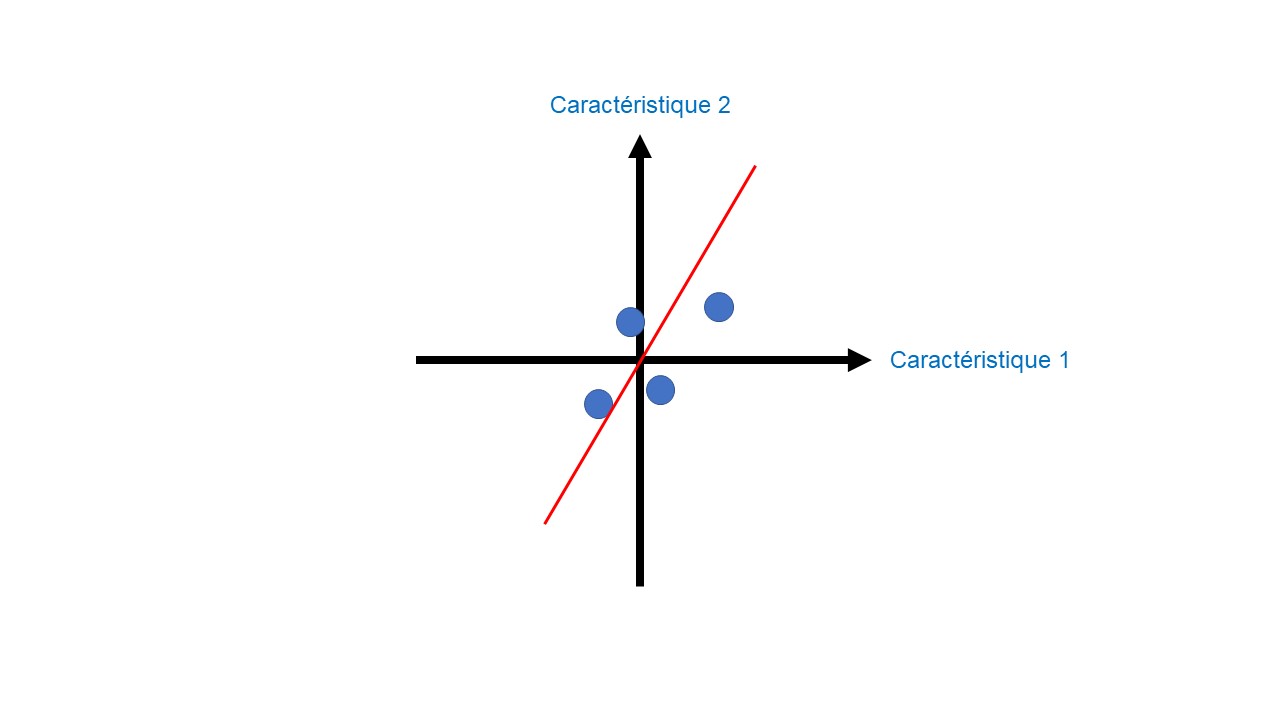
Une fois l’ensemble des étapes précédentes réalisées, nous traçons une droite passant par l’origine (Figure 4). Cette droite subit alors une rotation afin de trouver la meilleure droite passant par l’origine.
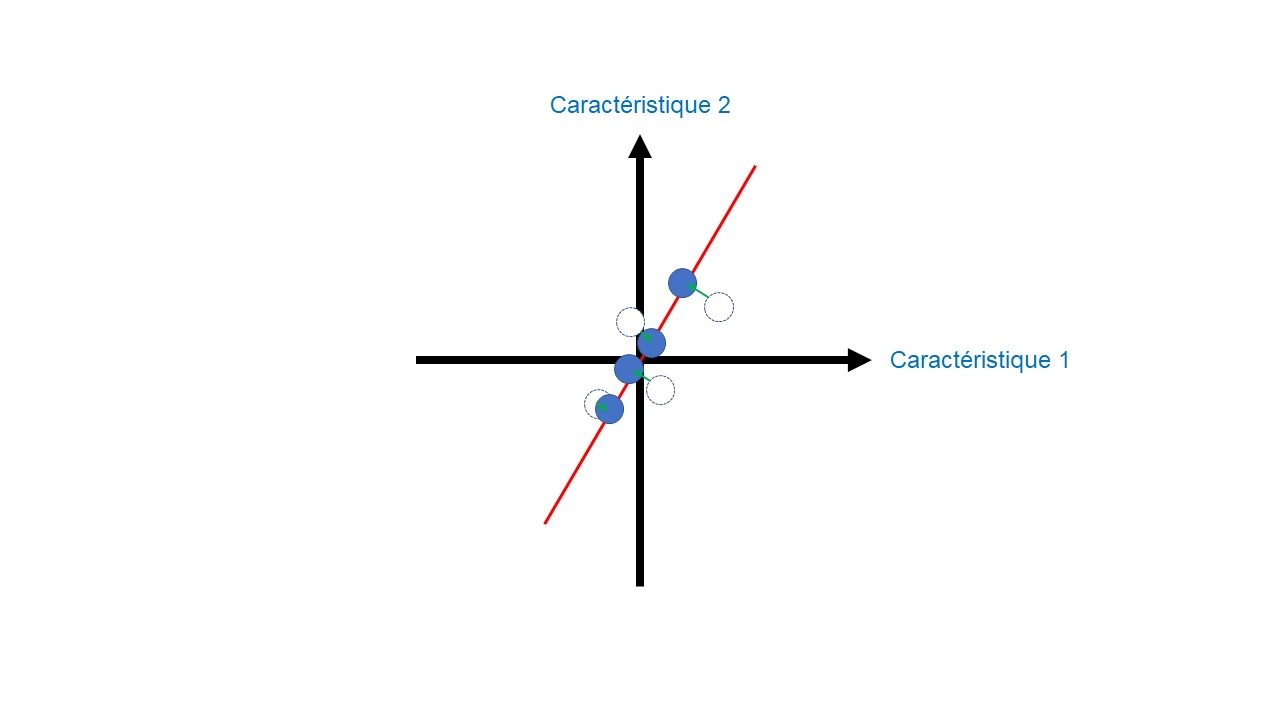
Pour quantifier la qualité de cette droite, nous projetons les données sur celle-ci (Figure 5). L’objectif est de trouver la droite qui maximise les distances entre les données projetées et l’origine.
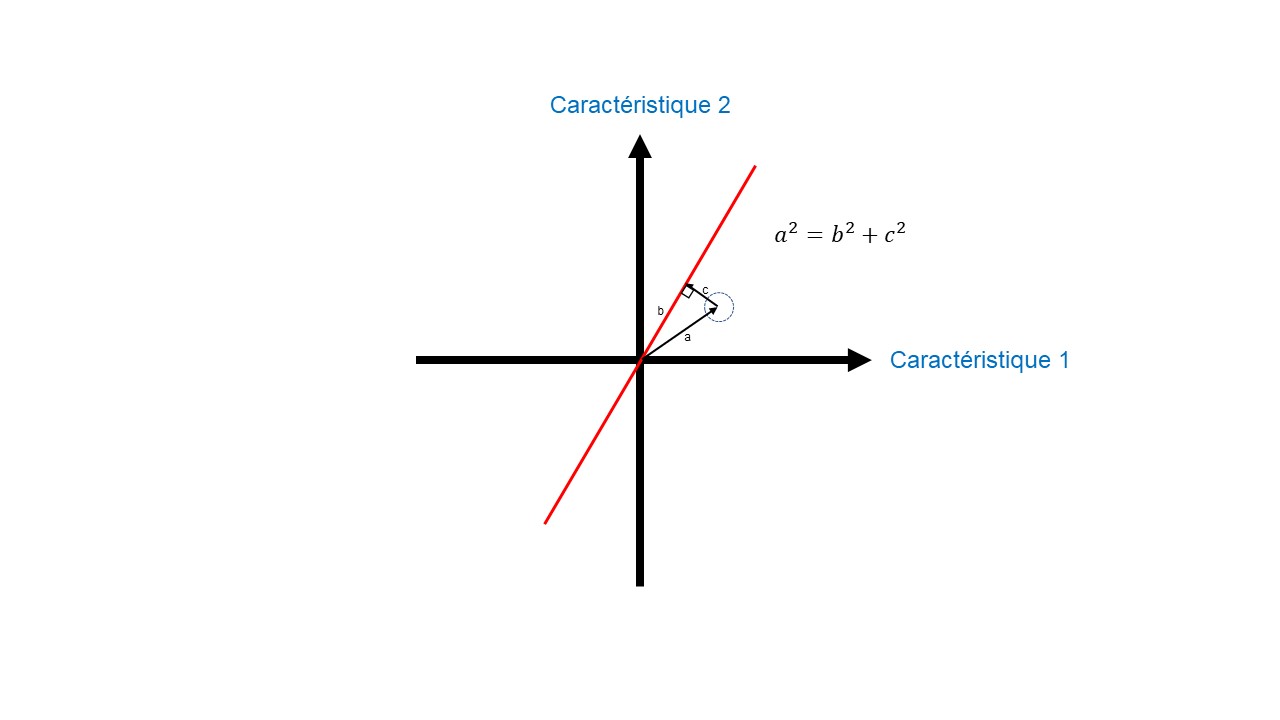
Cela revient à minimiser les distances entre les données non projetées et la droite. D’un point de vue géométrique, cela s’explique par le théorème de Pythagore (Figure 6). Si j’augmente les distances entre les données projetées et l’origine (distance b_Figure 6), cela revient à diminuer les distances entre les données non projetées et la droite (distance c_Figure 6). L’inverse est également vrai. La variation de ces distances n’influence pas la distance entre nos données non projetées et l’origine (distance a_Figure 6).
Nous mesurons chaque distance entre nos données projetées et l’origine (distance b_Figure 6). Ensuite ces distances sont mises au carré pour que les valeurs négatives n’annulent pas les valeurs positives. On préserve ainsi l’ensemble des variations de nos données. Enfin, l’ensemble de ces valeurs carrées est sommé pour trouver la somme des carrés des distances (valeur SS_Figures 7 et 8), aussi appelé valeur propre.
L’objectif est de maximiser cette valeur propre afin de déterminer la meilleure droite. Cette meilleure droite est aussi appelée la composante principale (PC).

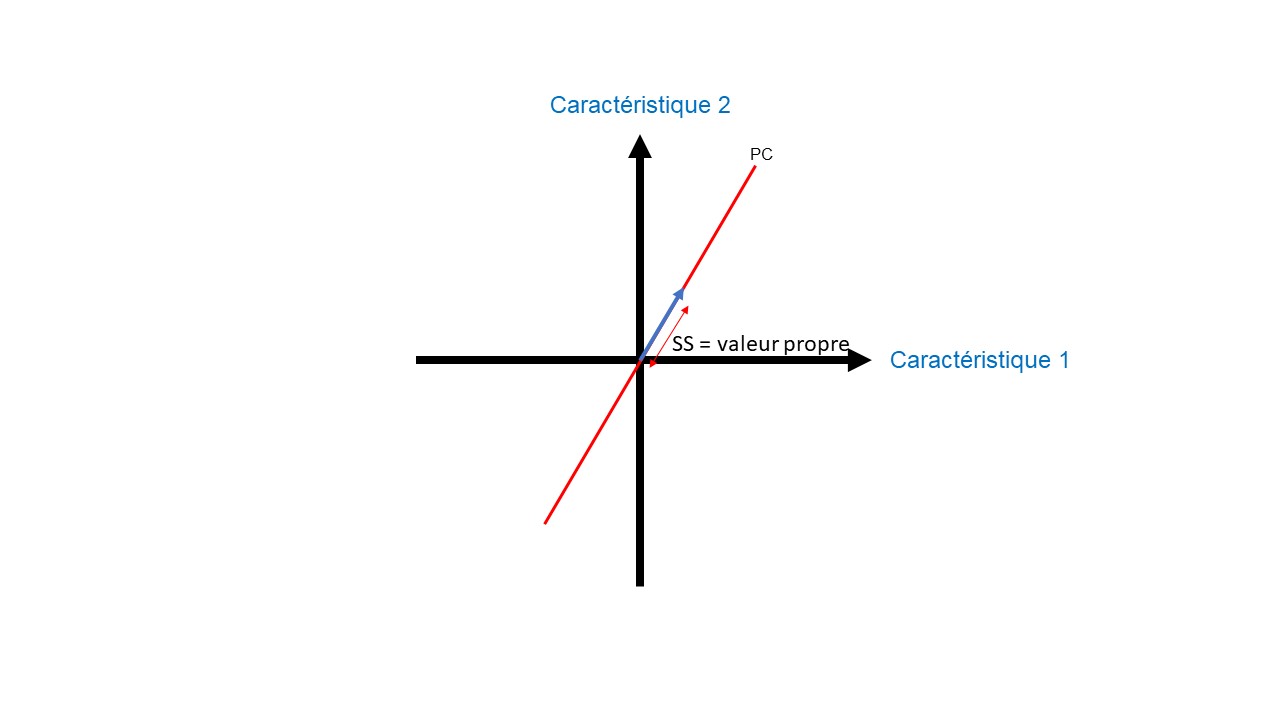
Le même travail est effectué sur les autres dimensions pour trouver les autres composantes principales. Toutes les composantes principales passent par l’origine et sont perpendiculaires les unes aux autres (Figure 9).
En définitive, nous obtenons des vecteurs propres (flèche bleue_Figure 9) partant de l’origine, de direction PC et ayant comme longueur (norme) la valeur propre.
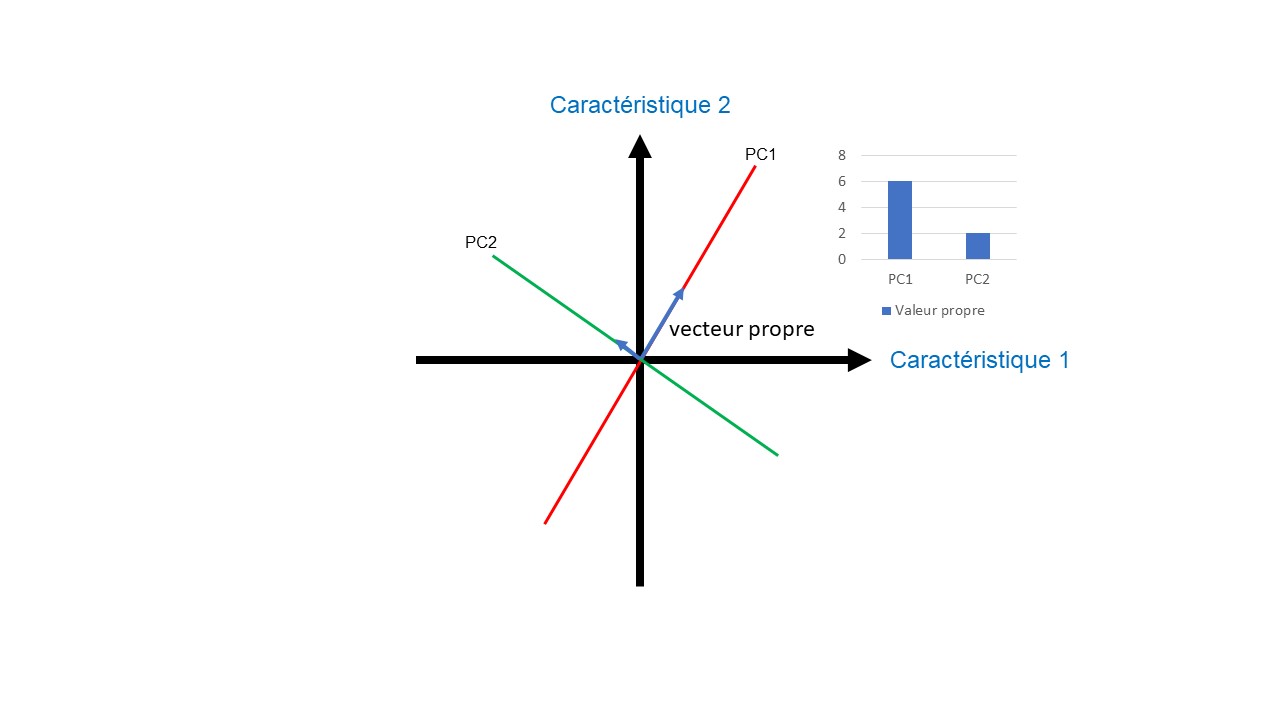
Cependant dans certaines situations, le vecteur propre peut prendre comme longueur la racine carrée de la valeur propre de la composante principale appelée la valeur singulière. On dit alors que la PCA utilise la décomposition en valeurs singulières (SVD).
Hierarchisation des composantes principales
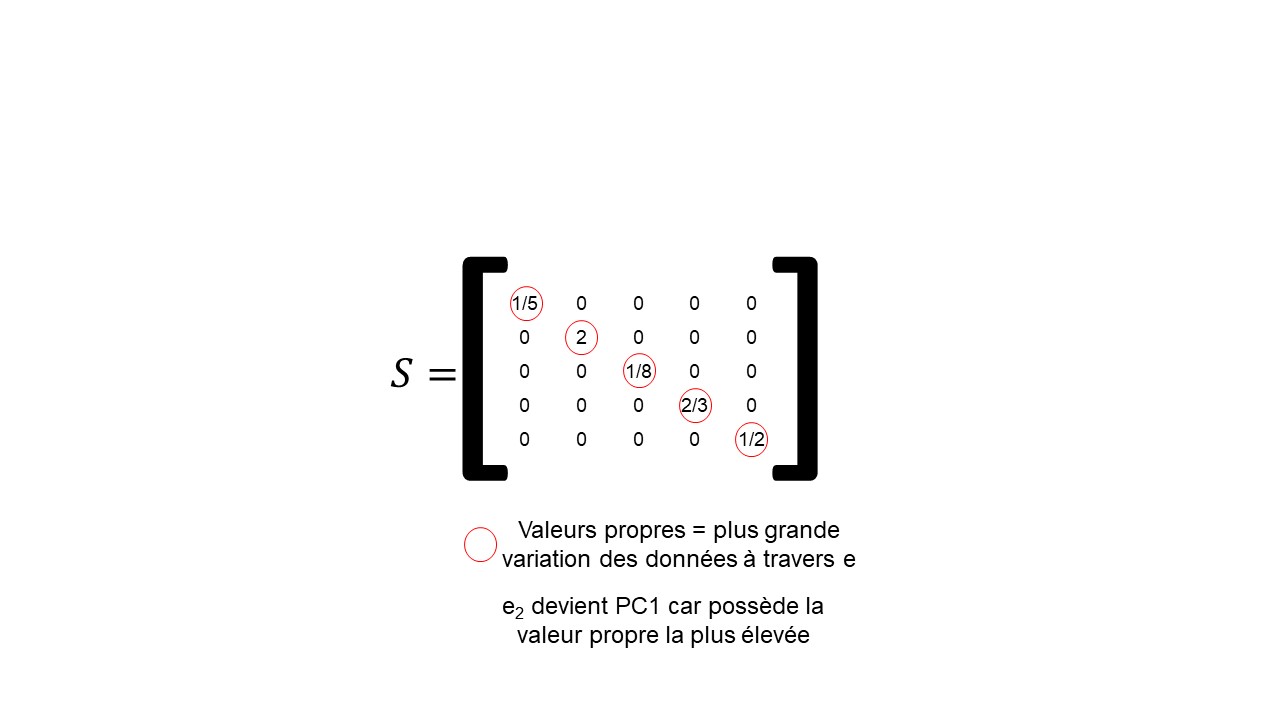
Dans cette dernière étape, nous réalisons un graphique linéaire appelé graphique en éboulis (scree plot) des valeurs propres afin de déterminer la hiérarchie des composantes principales (Figure 9A). La valeur propre qui a la valeur la plus élevée, correspond à la PC1 puis la suivante à la PC2, etc.
Dans certaines situations, des composantes principales de faibles valeurs propres peuvent être éliminées afin de diminuer le nombre de dimensions seulement si certaines composantes principales se détachent par leur variation prédominante par rapport aux autres. La PCA met majoritairement l’accent sur les premières composantes principales. Un seuil de 70% de variabilité commune est en général admis, cependant cette valeur demande discussion.
Les dernières composantes principales sont parfois utilisées pour détecter les valeurs aberrantes du jeu de données et pour certaines applications de l’analyse d’images.
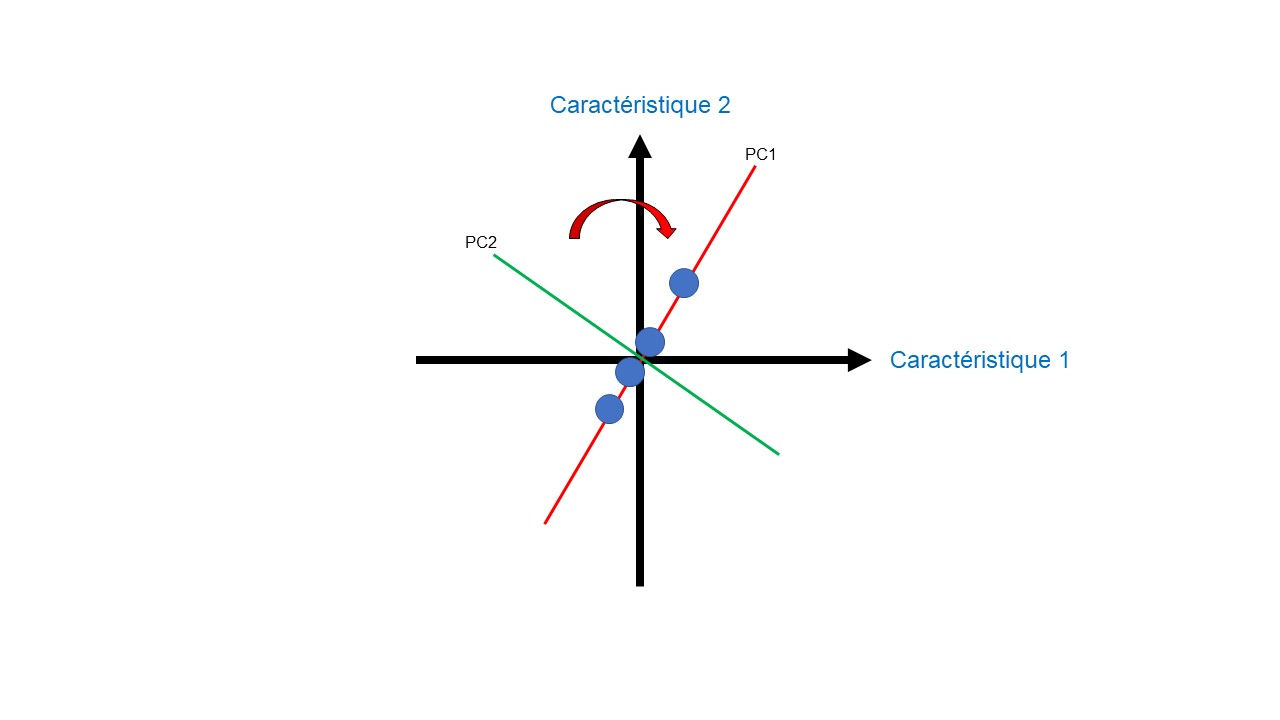
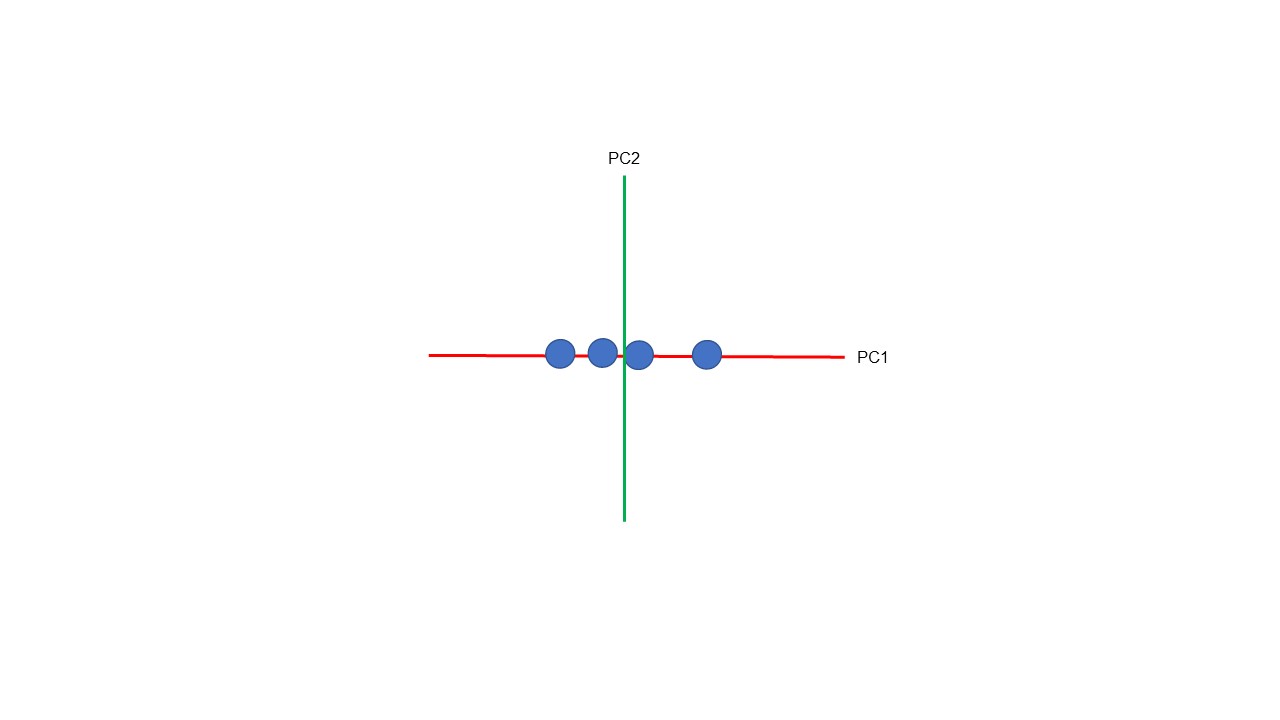
Au terme de l’analyse, quand la visualisation en 2D ou en 3D est nécessaire, une dernière étape peut être réalisée. Pour cela une rotation de l’espace vectoriel selon l’axe PC1 peut être réalisée (Figure 10, 11).

Approche numérique de l’analyse en composantes principales
L’utilisation d’une approche numérique peut permettre de comprendre cet algorithme. Cette approche reprend les trois étapes vues dans l’approche géométrique : le centrage des données par rapport à l’origine, la détermination des composantes principales et enfin la hiérarchisation des composantes principales.
Centrer nos données par rapport à l’origine
La première étape consiste à soustraire la moyenne de chaque variable du jeu de données pour centrer les données autour de l’origine.
Composantes principales dans une base orthonormée et valeurs propres
La matrice de covariance des données, les facteurs de modification de taille associés aux vecteurs propres (=valeurs propres) et les vecteurs propres de la matrice de covariance sont par la suite calculés (Figure 12).

Chacun des vecteurs propres orthogonaux est normalisé pour être transformé en vecteur unitaire (Figures 13A, 13B, 13C).
Une fois cette étape réalisée, chacun des vecteurs propres unitaires mutuellement orthogonaux peut être interprété comme un axe.
Cela transforme la matrice de covariance en une forme diagonalisée avec les éléments diagonaux représentant la variance de chaque axe (Figure 8). Cette transformation est une transformation linéaire orthogonale. La transformation orthogonale préserve les longueurs des vecteurs et les angles entre eux.
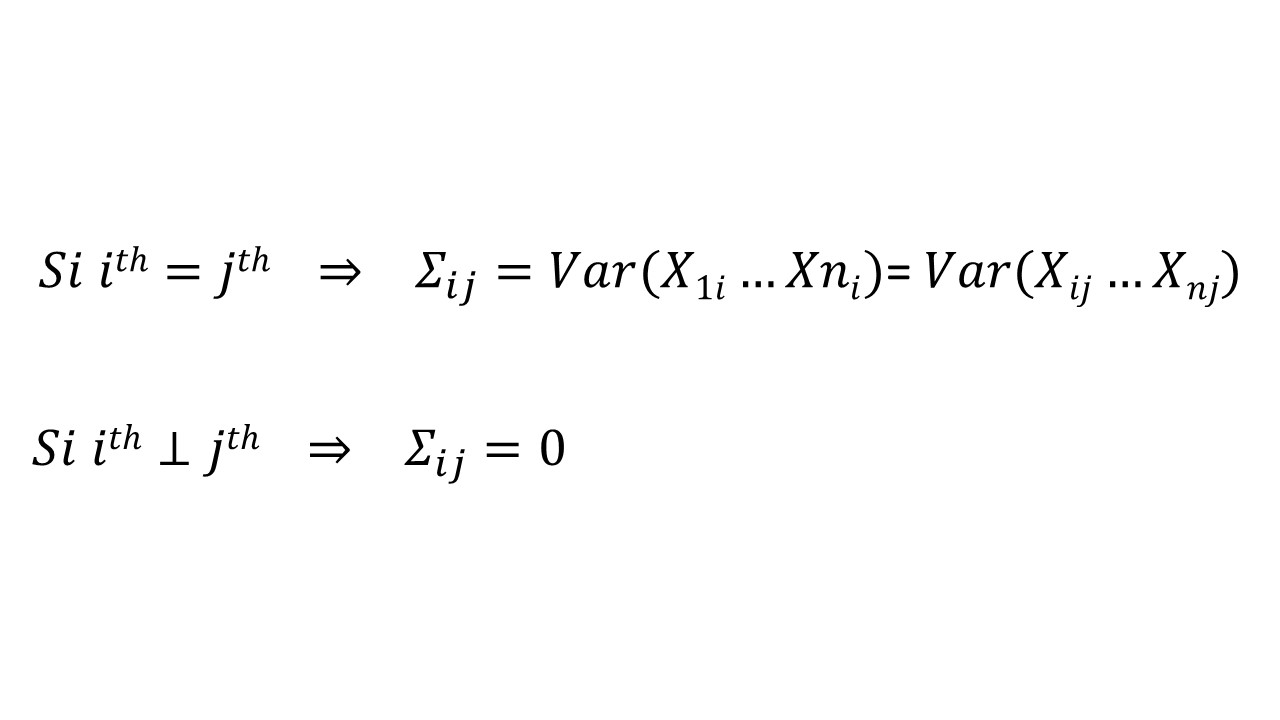
A : Valeur de la matrice de covariance si la i ème valeur et j ème valeur sont égales. Valeur de sigma si la i ème valeur et la j ème valeur sont indépendantes (non corrélées). 
B : Propriété symétrique de la matrice de covariance permettant selon la géométrie euclidienne de la projeter dans une base orthogonale E. Cette projection donne S. 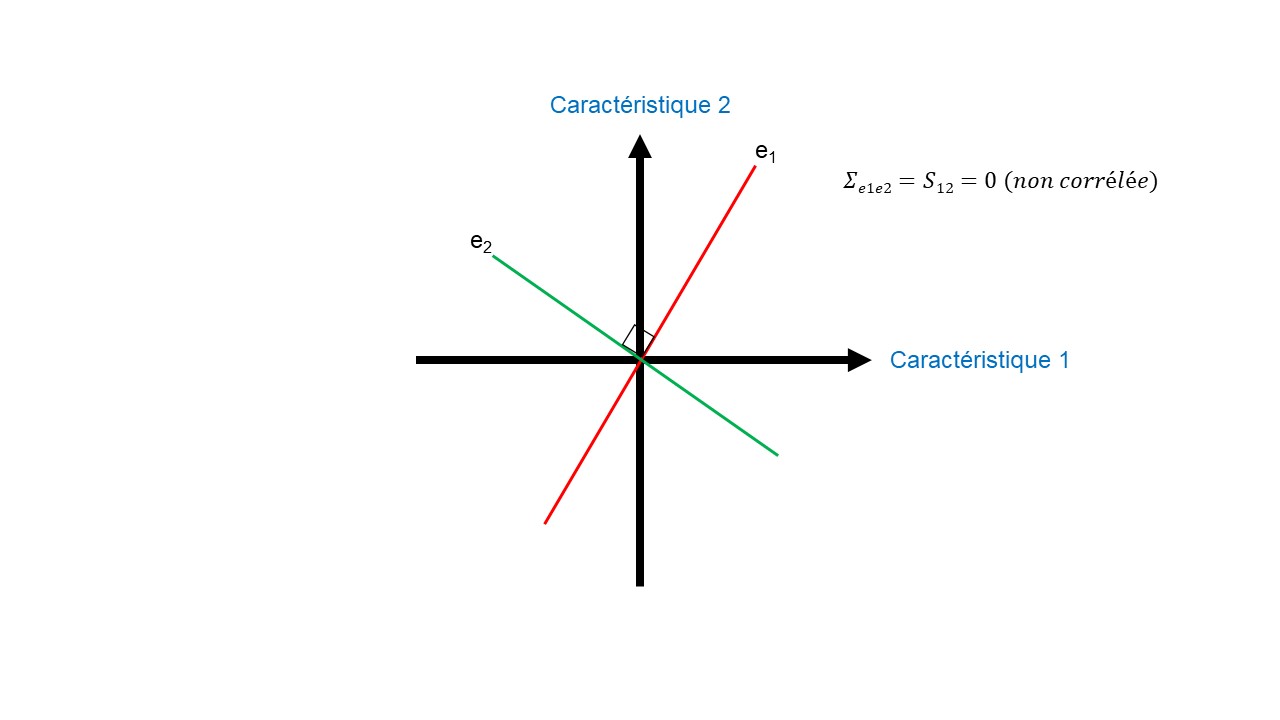
C : Représentation géométrique de la base orthogonale. e1 et e2 étant orthogonaux, la base S selon les dimensions e1 et e2 est égale à 0. On dit que e1 et e2 sont indépendantes (non corrélées).
Hierarchisation des composantes principales
La proportion de la variance que chaque vecteur propre représente peut-être calculée en divisant la valeur propre correspondante à ce vecteur propre par la somme de toutes les valeurs propres (Figure 14). Cette étape permet de hiérarchiser les composantes principales en PC1, PC2, etc.
Les approches géométrique et numérique présentées dans cet article sont applicables en raison du principe d’isomorphisme entre les vecteurs géométriques et numériques. Cela signifie qu’à chaque vecteur numérique correspond un vecteur géométrique et inversement ; et que les propriétés d’étirement et d’addition des vecteurs géométriques correspondent à celles des vecteurs numériques.
Conclusion sur l’analyse en composantes principales
Pour conclure, l’analyse en composantes principales standard remplace un ensemble de p variables par q nouvelles variables, appelées composantes principales. Ces composantes principales sont des combinaisons linéaires non corrélées des variables d’origines (centrées).
La première composante principale (PC1) est la combinaison linéaire de la variance maximale (avec pour coefficient un vecteur de norme unitaire). Les composantes principales suivantes sont les combinaisons linéaires de variance maximale, mais avec l’exigence supplémentaire de corrélation nulle avec toutes les autres composantes principales (perpendicularité des composantes).
Comme on le sait, les vecteurs de coefficients qui définissent les composantes principales sont les vecteurs propres de la matrice de covariance des p variables (ou de matrice de corrélation, si les variables sont standardisées). Chaque valeur propre de la matrice de covariance est la variance de la composante principale définie par le vecteur propre correspondant. Les vecteurs propres et les composantes principales ne définissent que des directions.
Donc l’analyse en composantes principales est un outil exploratoire majeur. Elle peut être utilisée pour extraire des caractéristiques importantes, pour détecter les valeurs aberrantes ou pour réduire la dimensionnalité des espaces de très grandes dimensions. Finalement elle semble être un atout majeur face à la malédiction de la dimensionnalité. De plus, comme nous le verrons dans un second article, son utilisation dans de nombreux domaines a amené les chercheurs à la modifier pour s’adapter aux données et aux objectifs à atteindre.

![Spark 3 : à la découverte des RDD [Part 2]](https://penseeartificielle.fr/wp-content/uploads/2022/02/fire-1905608_1280-218x150.jpg)
![Installation de Spark 3 sous Windows [Part 1]](https://penseeartificielle.fr/wp-content/uploads/2022/02/pexels-fabiano-rodrigues-1662298-218x150.jpg)
