Le Fizz Buzz est un petit test utilisé essentiellement en 2007 lors des entretiens de candidats développeurs.
Si l’exercice est simple, les résultats de l’époque sont étonnamment faibles : 99.5 % des candidats ont des difficultés à le résoudre ! En quoi consiste ce test, et comment le résoudre avec du deep learning (ce qui ne sert strictement à rien, disons-le dès à présent) ? C’est là qu’intervient fizzbuzz tensorflow !
Le test Fizz Buzz
L’énoncé du Fizz Buzz est généralement donné en ces termes : « rédigez un programme informatique qui affiche les nombres de 1 à 100 dans l’ordre, en remplaçant les multiples de 3 par le mot Fizz, les multiples de 5 par Buzz, et les multiples de 15 par FizzBuzz« .
De manière très simplifiée, il faut donc aboutir au pseudo algorithme suivant :
DE 1 A 100 FAIRE
SI multiple de 15 AFFICHER FizzBuzz
SINON SI multiple de 5 AFFICHER Buzz
SINON SI multiple de 3 AFFICHER Fizz
SINON afficher le nombre
A noter que résoudre « multiple de 3 ou de 5 » avant 15 amène une complication que l’on peut éviter en inversant les vérifications !
Ce genre d’exercice s’est largement démocratisé dans les années 2010, et aujourd’hui il est très fréquent d’avoir des problèmes à résoudre avant un entretien ou… pendant.
Plusieurs plateformes ont ainsi vu le jour pour mettre à l’épreuve nos compétences. Par exemple, la Battle Dev permet de s’exercer et de se confronter à d’autres développeurs, CodinGame est réputé pour ses jeux qu’il vous fait imaginer, SkillValue propose de valoriser/valider ses compétences, etc…
Mise en garde sur le deep learning
Maintenant que vous connaissez l’exercice et avez une bonne idée de comment le résoudre en quelques lignes, vous allez sûrement vous demander… pourquoi utiliser du deep learning ? Pourquoi se compliquer la vie ?

La raison est toute simple : l’objectif de cet article est de démontrer, comme l’a fait Joel Grus, qu’avoir recours aux réseaux de neurones n’est pas la solution à tous les problèmes ! Ce n’est pas parce que l’on parle constamment d’intelligence artificielle qu’il faut l’inclure dans tous les projets. De nombreux algorithmes de machine learning classiques (comprendre par là, qui datent de plusieurs années) sont encore tout à fait pertinents et obtiennent de meilleurs résultats que les réseaux de neurones !
C’est le cas, par exemple, du problème des survivants au Titanic, ou encore de FizzBuzz…
Néanmoins, l’approche du deep learning est possible, et même si elle ne permet (quasiment) jamais d’atteindre un score de prédiction de 100%, elle reste pertinente et instructive.
D’ailleurs, comme le conclut Joel en constatant les erreurs de son algorithme, il aurait dû utiliser plus de neurones et de couches cachées !!! (c’est une blague, ne le faites pas)
Travaux pratiques : réalisez un fizzbuzz tensorflow
On a donné le sujet, à vous de programmer, car maintenant on va donner la solution pas à pas !
Comme d’habitude, vous pourrez retrouver l’intégralité du projet sur notre GitHub.
1) Préparation de l’environnement
- Téléchargez Python 3 si ce n’est pas déjà fait, en l’ajoutant bien au PATH.
- Ouvrez une fenêtre de commande Windows et saisissez les lignes suivantes
pip3 install numpy pip3 install tensorflow
Numpy est une librairie permettant de travailler en Python avec les nombres (et plus précisément des vecteurs, utilisés par TensorFlow).
TensorFlow, pour sa part, est le framework de Google spécialisé dans le Deep Learning. Il comprend les réseaux de neurones, que nous allons utiliser ici.
2) Préparation des données
On va commencer par écrire une méthode qui permet de résoudre le FizzBuzz. Le but d’un algorithme de Deep Learning étant de prédire, il ne serait pas pertinent de valider notre entraînement sur les nombres de 1 à 100 (qui est le but final de l’exercice). On va donc entraîner l’algorithme sur les nombres de 101 à 1024 (par simplicité).
# Imports import numpy as np import tensorflow as tf # Longueur de la représentation binaire NUM_DIGITS = 10
Pour représenter les nombres en entrée, on va les encoder dans un vecteur de 0 et de 1 représentant leur décomposition en base 2. Par exemple, 15 sera représenté par [1,1,0,1] (1*8 + 1*4 + 0*2 + 1*1). Pour que tous les nombres aient la même représentation en terme de longueurs, on ajoutera des 0 devant.
# Converti un nombre en sa décomposition binaire
def binary_encode(i, num_digits):
return np.array([i >> d & 1 for d in range(num_digits)])
Et on va également créer un vecteur de sortie, qui servira à dire si on doit afficher le nombre, Fizz, Buzz ou FizzBuzz :
def fizz_buzz_encode(i):
if i % 15 == 0: return np.array([0, 0, 0, 1])
elif i % 5 == 0: return np.array([0, 0, 1, 0])
elif i % 3 == 0: return np.array([0, 1, 0, 0])
else: return np.array([1, 0, 0, 0])
On peut alors initialiser notre base d’apprentissage, qui va contenir tous les nombres de 101 à 1024 (représentés en binaire) trX et la sortie associée trY.
trX = np.array([binary_encode(i, NUM_DIGITS) for i in range(101, 2 ** NUM_DIGITS)]) trY = np.array([fizz_buzz_encode(i) for i in range(101, 2 ** NUM_DIGITS)])
3) Création du réseau de neurones avec TensorFlow
On va utiliser 100 neurones (arbitrairement) dans la couche cachée. La couche d’entrée comportera autant de neurones qu’il y a d’entrées correspondant à chaque nombre (donc 10 puisqu’on a converti en binaire).
A noter que la conversion en binaire permet d’éviter un gros problème : 100 > 1. Si on ne faisait pas la conversion, dans le calcul du réseau de neurones on aurait que l’entrée 100 est beaucoup plus importante que l’entrée 1 et le réseau sacrifierait ses capacités sur le chiffre 1 pour faire juste au nombre 100 (ce qu’on veut éviter).
La sortie, quant à elle, est de taille 4 puisqu’il y a 4 valeurs possibles (on aurait pu se contenter de 2 valeurs en réalité).
Initialisons les variables pour TensorFlow et les poids à passer au réseau :
# Les poids seront initialisés au hasard
def init_weights(shape):
return tf.Variable(tf.random_normal(shape, stddev=0.01))
# Perceptron à 1 couche utilisant ReLu comme fonction d'activation
# Softmax est appliqué en sortie pour la fonction de coût (pour convertir la sortie en probabilité)
def model(X, w_h, w_o):
h = tf.nn.relu(tf.matmul(X, w_h))
return tf.matmul(h, w_o)
# Nos variables
X = tf.placeholder("float", [None, NUM_DIGITS])
Y = tf.placeholder("float", [None, 4])
# Nombre de neurones dans la couche cachée
NUM_HIDDEN = 100
# Génération des poids
w_h = init_weights([NUM_DIGITS, NUM_HIDDEN])
w_o = init_weights([NUM_HIDDEN, 4])
Comme indiqué dans le code, on va utiliser la fonction d’activation ReLU qui a pour particularité de ne se déclencher que pour les nombres positifs (on enlève tous les négatifs) et ne modifie pas la valeur courante du neurone. Elle est donc utile pour diminuer le nombre de variables dont dépend un système.
Il nous faut également choisir une fonction de coût, qui servira à quantifier l’écart entre notre prédiction et la valeur attendue. De manière traditionnelle, on va recourir à la cross-entropy avec softmax (qui transforme les valeurs de sortie en probabilité). Il faut aussi indiquer quel algorithme de mise à jour des poids on va utiliser, soit ici la descente de gradient vue dans le focus sur le perceptron.
# La prédiction de y sera donnée en fonction de x grâce au modèle py_x = model(X, w_h, w_o) # Fonction de coût et stratégie de mise à jour des poids cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=py_x, labels=Y)) train_op = tf.train.GradientDescentOptimizer(0.05).minimize(cost)
Pour obtenir un résultat tangible, enfin, on considérera que la prédiction du réseau sera la sortie avec la plus haute prédiction. Par exemple, si le réseau indique 40% Fizz et 42% Buzz alors le message affiché sera Buzz.
predict_op = tf.argmax(py_x, 1)
# Conversion en sens inverse de fizzbuzz : la prédiction finale devient le mot à afficher
def fizz_buzz(i, prediction):
return [str(i), "fizz", "buzz", "fizzbuzz"][prediction]
4) Entraînement de l’algorithme
Notre algorithme va réaliser 10 000 époques durant lesquelles il va prendre aléatoirement 128 nombres en entrée, prédire la sortie, puis à la fin (des 128 entrées) mettre à jour les poids en fonction de l’erreur commise.
BATCH_SIZE = 128
On ouvre une session TensorFlow, qui est le moyen traditionnel de travailler avec le framework : elle permet d’allouer des ressources (CPU, GPU, machine) à TensorFlow et contient donc les calculs intermédiaires et les variables :
with tf.Session() as sess:
tf.initialize_all_variables().run()
Attention, car une fois sortie de la boucle, la session est perdue et vous n’avez plus accès à tous les résultats intermédiaires !
On va boucler sur nos époques, en prenant aléatoirement les nombres dedans et en entraînant l’algorithme à la fin :
for epoch in range(10000):
# Mélange des données aléatoire
p = np.random.permutation(range(len(trX)))
trX, trY = trX[p], trY[p]
# Entraînement par batch de 128 lignes
for start in range(0, len(trX), BATCH_SIZE):
end = start + BATCH_SIZE
sess.run(train_op, feed_dict={X: trX[start:end], Y: trY[start:end]})
# Affichage au fur et à mesure de la précision
print(epoch, np.mean(np.argmax(trY, axis=1) ==
sess.run(predict_op, feed_dict={X: trX, Y: trY})))
5) Prédiction du résultat
Enfin, on va demander à notre algorithme entraîné de ses 10 000 époques de nous prédire les nombres de 1 à 100 :
numbers = np.arange(1, 101)
teX = np.transpose(binary_encode(numbers, NUM_DIGITS))
teY = sess.run(predict_op, feed_dict={X: teX})
output = np.vectorize(fizz_buzz)(numbers, teY)
print(output)
On obtient ainsi le tableau de prédictions de notre modèle deep learning du fizzbuzz !
Si on veut le comparer aux vrais résultats attendus, il suffit d’ajouter les lignes suivantes :
actuals = [fizz_buzz(i, fizz_buzz_encode(i).argmax()) for i in numbers]
for i, (predicted, actual) in enumerate(zip(output, actuals)):
if predicted != actual:
print("{0} {1} {2}".format(i+1, predicted, actual))
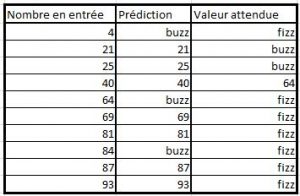
On obtient alors des résultats satisfaisants, de l’ordre de 5 à 10 erreurs pour 100 prédictions… Résultats bien meilleurs avec du Machine Learning, et encore meilleurs avec de l’algorithmie classique !
Pour vous amuser, vous pouvez essayer d’augmenter le nombre de neurones, le nombre de couches, de changer les modèles, ou encore d’appliquer cet exemple à d’autres exercices (le XOR par exemple).
Crédit de l’image de couverture : Willy Stöwer – Public Domain)


![Spark 3 : à la découverte des RDD [Part 2]](https://penseeartificielle.fr/wp-content/uploads/2022/02/fire-1905608_1280-218x150.jpg)
![Installation de Spark 3 sous Windows [Part 1]](https://penseeartificielle.fr/wp-content/uploads/2022/02/pexels-fabiano-rodrigues-1662298-218x150.jpg)
