Introduction
La pneumonie
L’Organisation Mondiale de la Santé (OMS) et le Fond International des Nations Unies pour l’Enfance (Unicef) caractérisent dans un rapport publié en 2006 la pneumonie de l’enfant, comme un fléau oublié. Dans ce rapport, la pneumonie est définie comme « une forme grave d’infection virale, bactérienne ou fongique aiguë des voies respiratoires basses qui s’attaque spécifiquement aux poumons ».
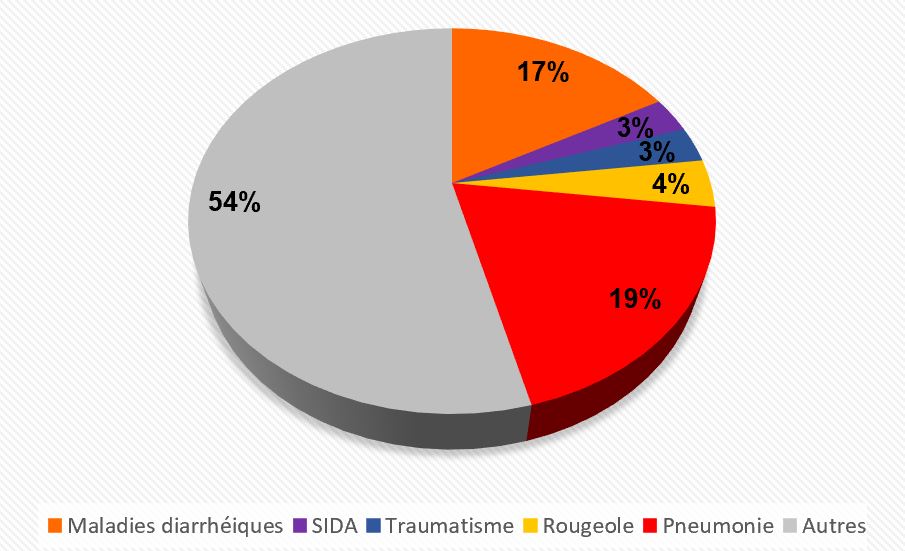
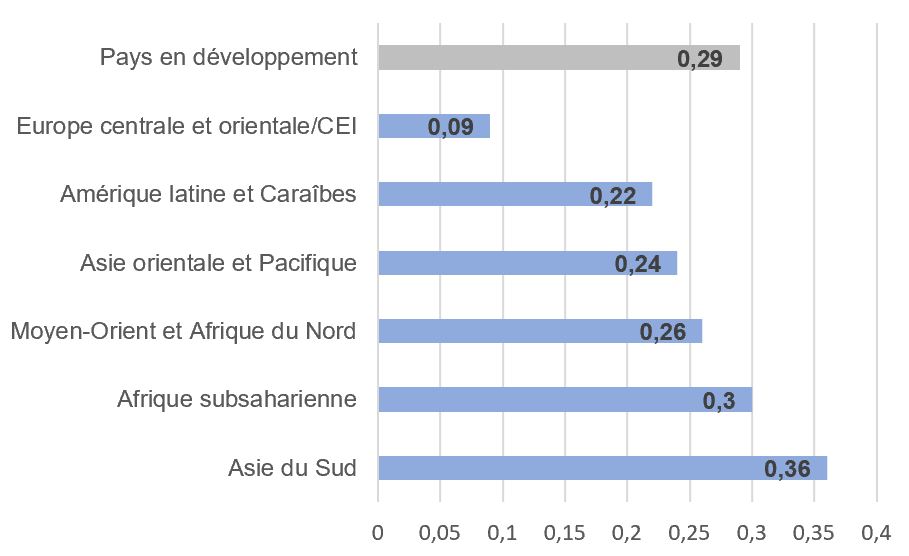
Cette infection est la première cause de mortalité chez les enfants de moins 5 ans. En effet, elle est responsable de 19% des décès infantiles chaque année (Figure 1A). Dans les pays en développement comme l’Afrique subsaharienne et l’Asie du Sud, le nombre d’épisodes par enfant et par an est supérieur aux autres régions du monde (Figure 1B). Dans ces pays, une plus grande proportion des enfants souffre de dénutrition ou est victime d’autres maladies comme le SIDA ou la rougeole, à l’origine d’un affaiblissement de leur système immunitaire. Un certain nombre de facteurs environnementaux comme l’entassement des familles dans des logements exigus, le tabagisme des parents et la pollution de l’air à l’intérieur des locaux, ont été notés dans le rapport de l’OMS de 2006 comme pouvant augmenter le risque pour les enfants de contracter une pneumonie et en aggraver les conséquences.
Le diagnostic précoce de cette infection permettrait une prise en charge rapide des patients et une diminution du nombre de décès.
Les symptômes de cette maladie évoluent en fonction de l’âge et de l’origine de l’infection. Les symptômes de la pneumonie virale apparaissent progressivement et peuvent s’aggraver avec le temps. Cependant, une pneumonie d’origine bactérienne peut généralement se manifester par une fièvre importante et une accélération de la respiration. Un certain nombre d’autres symptômes sont observés chez l’enfant comme une toux, une respiration sifflante, des céphalées (maux de tête) et une anorexie.
Après observation d’une partie ou de l’ensemble de ces symptômes par un professionnel de santé, d’autres examens viennent se rajouter au diagnostic. La localisation et l’expansion de la maladie peuvent être déterminées par des examens de laboratoire et la radiographie thoracique. Cette dernière est une technique d’imagerie médicale utilisant les rayons X. Effectivement, les rayons X projetés à travers le thorax du patient vont être captés par une plaque numérique. En fonction du tissu traversé, les faisceaux de rayons X vont être plus ou moins atténués. Les tissus mous comme le cœur vont apparaître en gris; les tissus denses comme les os vont apparaître en blanc et les parties contenant de l’air comme les poumons apparaissent en noir.
L’analyse de ces images obtenues par radiographie thoracique nécessite une analyse précise par un médecin ou un ensemble d’experts médicaux. La prise de décision du médecin peut être guidée par de nouveaux outils permettant un diagnostic plus précis de l’infection et une prise en charge plus rapide du patient.
Les réseaux convolutifs
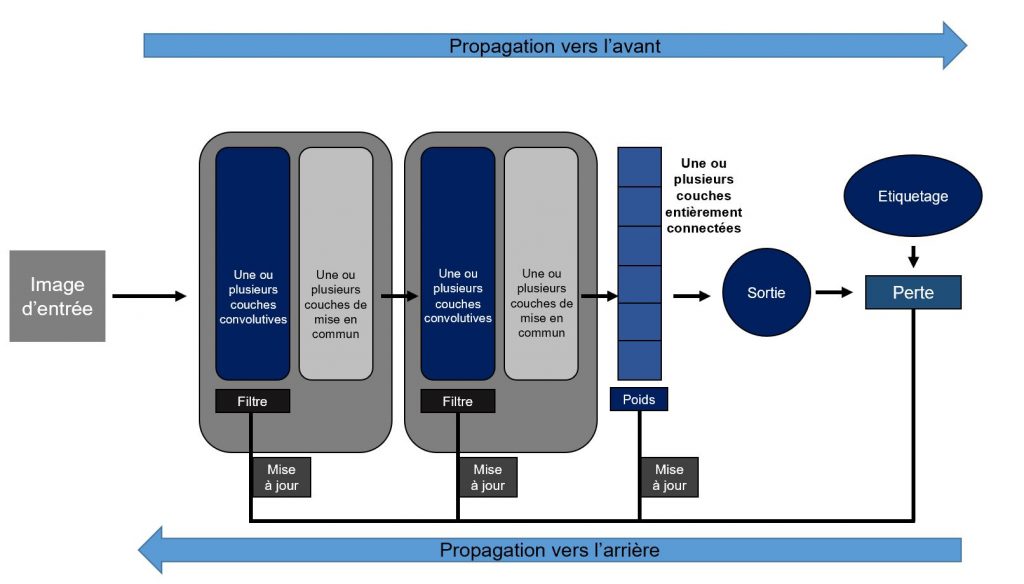
Une des innovations les plus importantes de notre décennie est la vision par ordinateur. Cette prouesse technologique est permise par la création d’algorithmes nommés réseaux convolutifs (Convolutional Neural Networks, CNN).
Ces CNN sont des algorithmes de Deep Learning permettant de préserver la relation spatiale existante entre les différentes valeurs d’une matrice. Cette propriété principale des CNN a permis leur utilisation dans la reconnaissance d’images par l’extraction des caractéristiques de cette dernière.
Ces réseaux convolutifs sont composés de trois types de couches. Les couches de convolution et celles de mise en commun (pooling) impliquées dans l’extraction des caractéristiques de l’image. La couche entièrement connectée (fully connected layer) permettant la sortie d’une cartographie des caractéristiques extraites préalablement.
Cet algorithme permet d’analyser une grande quantité d’images en un temps limité ce qui pourrait constituer un apport majeur au domaine de l’imagerie médicale.
L’utilisation des réseaux convolutifs en radio-diagnostique
L’utilisation de nouvelles technologies dans le domaine de la radiologie est présente dans la littérature scientifique. Nombreuses sont celles utilisant des algorithmes d’apprentissage automatique (Machines Learning) comme la forêt d’arbres décisionnels (Random Forests) et la machine à vecteurs de support (SVM).
Cependant l’apprentissage automatique a ses limites. Le travail fastidieux d’extraction des caractéristiques lors de la préparation des données ne se retrouve pas pour les CNN. De plus, les algorithmes d’apprentissage automatique nécessitent une préparation préalable de la zone anatomique par une technique de segmentation.
En revanche, les algorithmes d’apprentissage profond (Deep Learning) sont beaucoup plus coûteux en calcul et nécessitent un jeu de données beaucoup plus important que ceux de l’apprentissage automatique.
L’apprentissage par transfert (transfert Learning) face à la pénurie d’images radiologiques étiquetées
Le faible nombre d’images radiologiques étiquetées dans le domaine médicale reste un défi majeur.
L’apprentissage par transfert (transfert Learning) a montré des performances intéressantes sur de faibles jeux de données.
Cette méthode consiste à transférer les paramètres appris par un CNN pré-entrainé sur un nombre de données important, vers un autre jeu de données souvent moins important et/ou à une autre tâche.
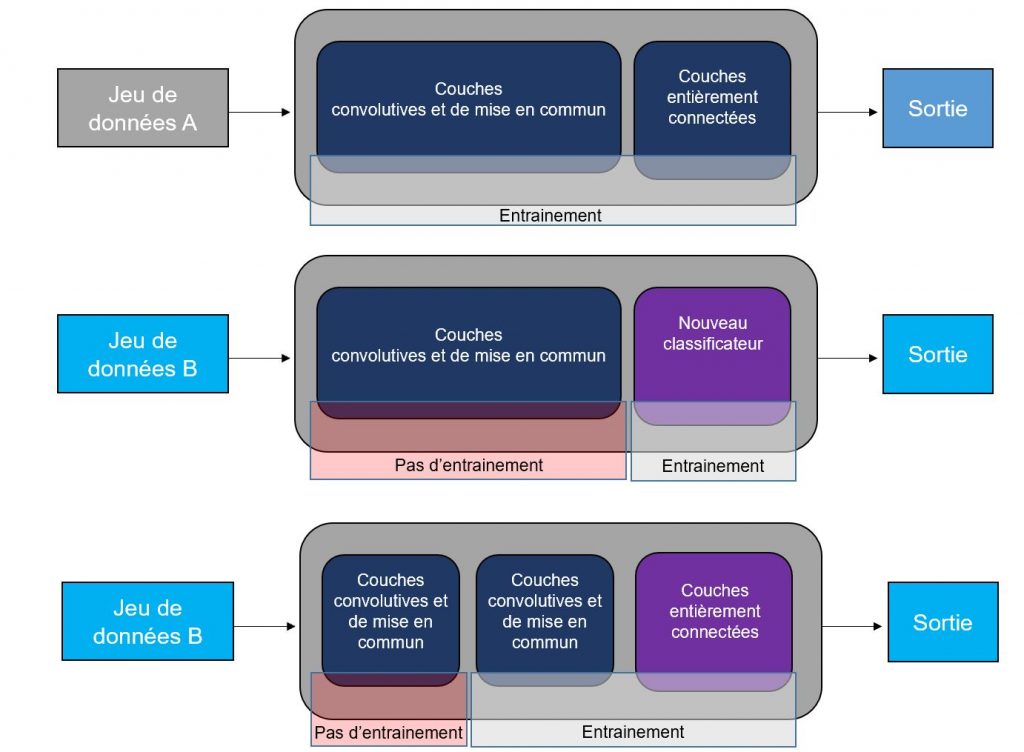
En haut : Réseau pré-entrainé sur un jeu de données A de très grande taille.
Au centre : Transfert du réseau pré-entrainé à un jeu de données B. Pour cette méthode, l’ancien classificateur (dernière couche permettant la prédiction) est remplacé par un nouveau, spécifique à la tache B. Et seuls les paramètres de cette dernière couche sont appris.
En bas : Transfert du réseau pré-entrainé à un jeu de données B. Pour cette méthode, un certain nombre de couches entièrement connectées est rajouté. Les paramètres de ces dernières couches et d’une partie du réseau pré-entrainé sont appris. (crédit : Maxime Masson – CC BY 3.0)
Dans cet article, je vais réaliser un réseau convolutif permettant de classer des images de radiographie thoracique d’enfants de 1 à 5 ans en fonction de la présence de pneumonie ou non.
Travaillant à partir d’un petit nombre d’images, j’utilise l’apprentissage par transfert. Le modèle utilisé provient de la librairie Keras. Il s’agit d’un réseau de classification d’images avec des poids formés sur ImageNet.
Matériel et méthode
Données
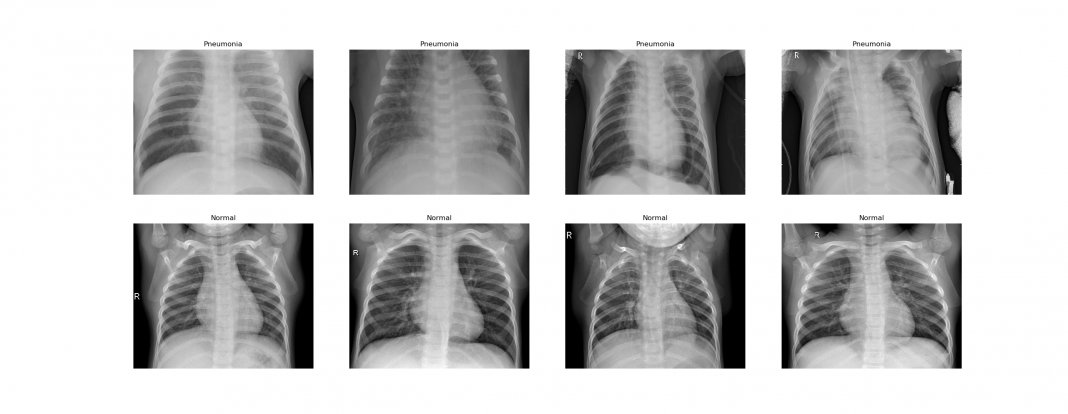
L’ensemble des données provient de la bibliothèque kaggle. Ces images radiographiques thoraciques antéro-postérieures ont été réalisées sur des cohortes rétrospectives de patients âgés de 1 à 5 ans, du Centre médical pour femmes et enfants de Guangzhou, ville de Hong Kong.
Toutes les images radiologiques ont été présélectionnées par suppression de toutes les données de mauvaise qualité ou illisibles. Par la suite, deux médecins experts ont procédé à l’étiquetage des données. Puis un troisième expert s’est assuré de la bonne classification.
Prétraitement des données pour le Transfert Learning
Division des données
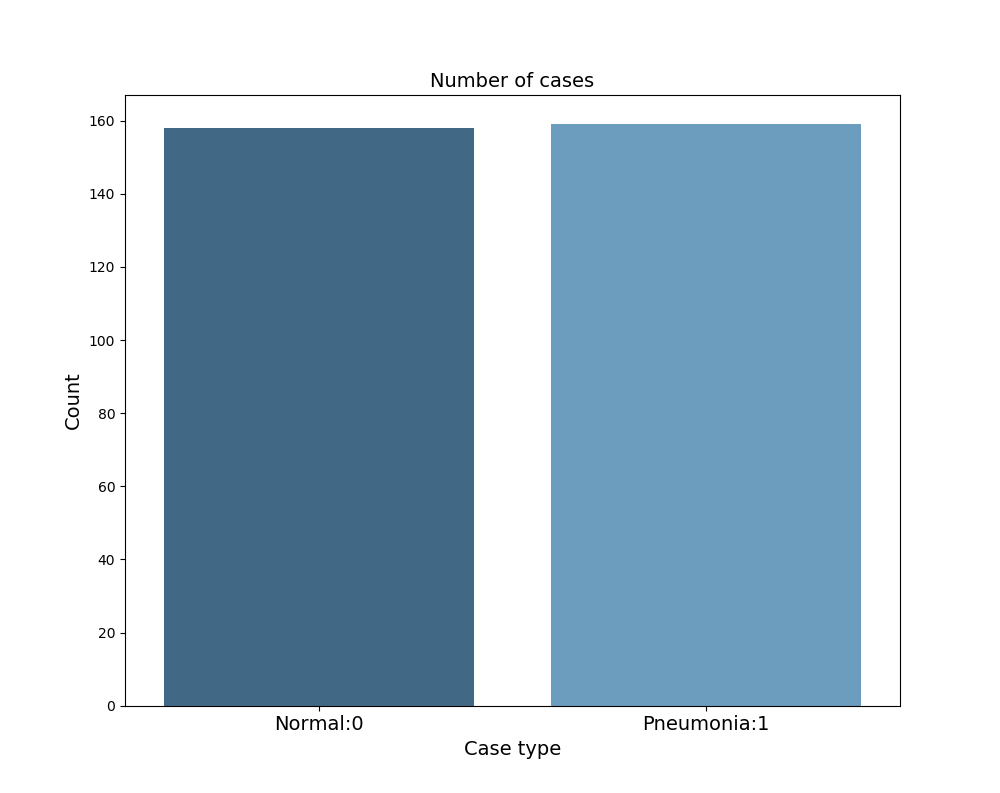
L’ensemble des données a été divisé en 3 jeux de données (80 :10 :10). Ce sont les données d’entraînement, les données de validation et les données de test. Les données d’entraînement permettent d’entraîner le model. Les données de validation, permettent de régler les hyper paramètres, comme le taux d’apprentissage et le nombre d’unités par couche, afin de sélectionner un modèle possédant la meilleure performance. Enfin, les données de test permettent l’évaluation finale de la performance du modèle. Ces 3 groupes possèdent la même proportion d’images radiographiques thoraciques sous le format JPEG de patients sains et souffrant d’une pneumonie virale ou bactérienne qui proviennent de la même distribution.
. 
Méthode d’optimisation : Normalisation
Les données d’entrées du jeu d’entraînement, de validation et de test ont subi une normalisation afin d’accélérer l’exécution de l’algorithme. La première étape est de remettre la moyenne à zéro ; la seconde de normaliser les variances des données d’entrée en définissant l’écart type à 1. Cela permet de rendre plus symétrique la fonction de coût. Cette dernière, correspondante à la fonction qui mesure la différence entre la valeur prédite et réelle de la sortie, est donc plus rapide à optimiser. Pour réaliser cette normalisation, l’intensité de chaque pixel a été divisée par 255.
Architecture du réseau utilisant le Transfert Learning
Modèle pré-entrainé
Le modèle pré-entrainé est Xception. Ce réseau de neurones convolutifs a été proposé par François Chollet dans « Xception: Deep Learning with Depthwise Separable Convolutions». La précision du modèle atteint 94.5% dans le top 5 et 79% dans le top 1 dans ImageNet. Sa profondeur est de 126 couches et possède 22 910 480 paramètres.
Transfert Learning
L’ensemble de données étant limité et le budget de calcul pas assez important pour tout entraîner de zéro, la décision d’utiliser l’apprentissage par transfert a été prise.
Afin de progresser plus rapidement, les poids du modèle déjà entraîné ont été transférés à notre tâche. L’apprentissage par transfert est utilisé pour transférer la connaissance d’un vaste ensemble de données (Imagenet) à notre propre jeu de données. Nous avons utilisé le modèle pré-entrainé Xception. La couche de sortie « softmax » a été remplacé par un nouveau classificateur « sigmoïde ». Une couche cachée de 32 unités pour le modèle 1 et de 256 unités pour le model 2 a été rajoutée, avec une fonction d’activation « relu ». Seuls les poids des deux dernières couches vont être appris. Car travaillant sur une base de données très faible, la décision de geler l’ensemble des couches du réseau pré-entrainé a été prise.
Optimisation de l’architecture neuronale
Les principaux problèmes retrouvés lorsqu’un faible nombre de données est utilisé pour entraîner un réseau convolutif, sont le biais et la variance.
Biais et variance
Définition
Le biais est un sous-ajustement sur les données et la variance est un sur-ajustement sur les données. Pour connaître ces deux paramètres nous devons regarder l’erreur sur le jeu d’entraînement et l’erreur sur le jeu de validation.
Si le taux d’erreurs sur le jeu de validation est très important par rapport à celui du jeu d’entraînement, on parle d’un sur-ajustement. Dans ce cas, le réseau ne se généralise pas aux données de validation. On dit que la variance est haute.
Si les taux d’erreurs sur le jeu d’entraînement et sur le jeu de validation sont éloignés de l’erreur optimale (erreur de Bayes) et que leur valeurs sont proches, on parle d’un sous-ajustement. Dans cette situation le biais est haut.
Au contraire, si les taux d’erreurs sur le jeu d’entraînement et sur le jeu de validation sont éloignés de l’erreur optimale (erreur de Bayes) mais que leurs valeurs sont éloignées, on dit qu’il y a un haut biais et une haute variance.
L’objectif recherché est d’avoir un taux d’erreurs sur les jeux d’entraînement de validation proche de l’erreur optimale (erreur de Bayes) et que leurs valeurs soient le plus proche possible, on dit qu’il y a un faible biais et une faible variance.
Priorités
Le premier paramètre à regarder est le biais. Si le biais est élevé alors plusieurs possibilités sont envisageables.
Par exemple, la création d’un réseau plus grand en augmentant le nombre de couches cachées ou en augmentant le nombre d’unités (neurones) par couches cachées ; l’augmentation du temps d’apprentissage en augmentant le nombre d’époque et en changeant d’algorithme d’optimisation ; le changement d’architecture du réseau utilisé.
Ce sont autant de caractéristiques sur lesquelles nous pouvons jouer.
Le second paramètre à regarder est la variance. Si la variance est élevée alors d’autres possibilités sont envisageables. L’augmentation des données, une architecture du réseau différente et les méthodes de régularisations sont d’autres caractéristiques sur lesquelles nous pouvons jouer.
Compromis biais variance
Dans l’aire du Deep Learning, modifier le biais en utilisant certaines méthodes n’aura pas beaucoup d’influence sur la variance et inversement. Cela nous permet de nous concentrer sur un des paramètres sans impacter l’autre.
Enrichissement des données
Une technique d’augmentation des données a été employée sur les données d’entraînement. Cette technique d’enrichissement est utilisée pour résoudre le problème de variance rencontré fréquemment quand le jeu de donnée est de petite taille. Effectivement, la variance entre les données d’entraînements et les données de validation a tendance à être plus importante lorsque l’on travaille avec peu de données d’entrées. Les images ont subi un recadrage de 0,2%, un zoom de 0,2%, une rotation horizontale de 20 degrés, un décalage de la hauteur et de la largeur de 0,2%. Les transformations ont été appliquées par calcul en utilisant la bibliothèque Keras pour Python (version 3.7).
Méthode de régularisation
Un sur-ajustement est dû à la prise en compte de l’ensemble des caractéristiques définissant les données d’entrée. Une caractéristique correspond aux motifs retrouvées chez une certaine classe d’images. Par exemple la présence d’oreilles pointues, de vibrisses sont autant de caractéristiques permettant de reconnaître que l’image est un chat. Cependant, un certain nombre de ces caractéristiques a peu d’impact sur l’identification de l’image. Pour poursuivre avec l’exemple de l’image d’un chat, la présence de tâches sur une images est une caractéristique à faible impact pour l’identification du chat, car certain en ont mais d’autres non. Le but de la régularisation est de diminuer l’impact de l’ensemble des caractéristiques. En globalisant cette diminution, ces caractéristiques qui avaient déjà peu d’impact se retrouvent presque annulées. Cela permet au réseau de garder seulement les caractéristiques principales afin d’obtenir une sortie optimale.
C’est ce qui est fait en utilisant la régularisation par abandon « Dropout » avec une valeur de 0,5. Cette méthode très utilisée en vision par ordinateur, permet d’appliquer à chaque couche une probabilité « Keep-prob » de garder ou non une unité.
Durant la phase de test, cette méthode ne peut être gardée, car ces données doivent fonctionner sur le réseau optimal. Cela ajoutera seulement du bruit à la prédiction. La sortie du réseau ne peut être aléatoire.
Malgré l’importante utilisation du Dropout, il est souvent intéressant d’entraîner le réseau neuronal dans un premier temps sans cette méthode de régularisation. Effectivement, cet outil peut affecter la visualisation de la diminution monotone de la fonction de coût.
Autres paramètres :
Fonction de coût
La fonction de coût « binary_crossentropy » a été utilisée. Cette fonction est souvent utilisée lorsqu’il n’y a que deux classes d’étiquettes.
Descente de gradient : ADAM (Adaptative Momentum estimation)
La méthode de descente de gradient utilisée est Adam. Cet algorithme d’optimisation est la technique de descente de gradient stochastique la plus utilisée en raison de son efficacité et de sa stabilité.
Nombre d’époques et taille du batch :
Après l’entraînement de nombreux modèles, une taille de lot (batch) de 32 exemples et un nombre d’époques de 50 ont été décidés. Le nombre de batch correspond au nombre de données d’éntrainement passant dans l’agorithme avant la mise à jour des paramètres. Et le nombre d’époques correspond au nombre de fois que l’ensemble des exemples d’entrainements passes dans l’agorithme.
Taux d’apprentissage :
Le taux d’apprentissage correspondant à la vitesse à laquelle les paramètres évoluent, a été fixé après de nombreuses itérations à 1*10-5.
Résultats
L’entraînement de plusieurs modèles de réseau convolutif, a conduit à la sélection de 2 d’entres eux : les modèles numéro 1 et 2 possédant respectivement 32 et 256 unités dans leur couche cachée.
L’analyse de l’évolution de la précision au cours des 50 époques a permis de contrôler le taux d’apprentissage des différents modèles (Figure 6A). Le modèle ayant le moins d’unités, possède une précision initiale et finale inférieure à celle du modèle 2. La précision initiale du modèle 1 est de 64% et sa précision finale est de 88,42% ; alors que celle du modèle 2 est de 81% pour la précision initiale et de 90,27% pour sa précision finale. Le plateau pour le modèle possédant le plus d’unités est atteint plus rapidement que pour le modèle 1, respectivement 2 époques et 10 époques.
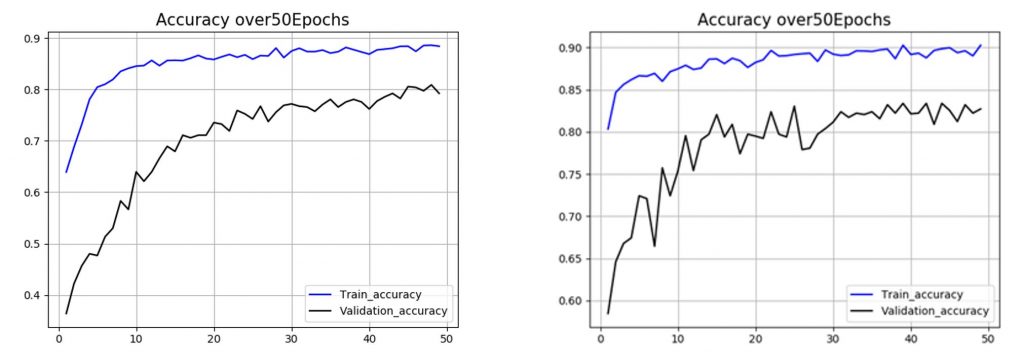
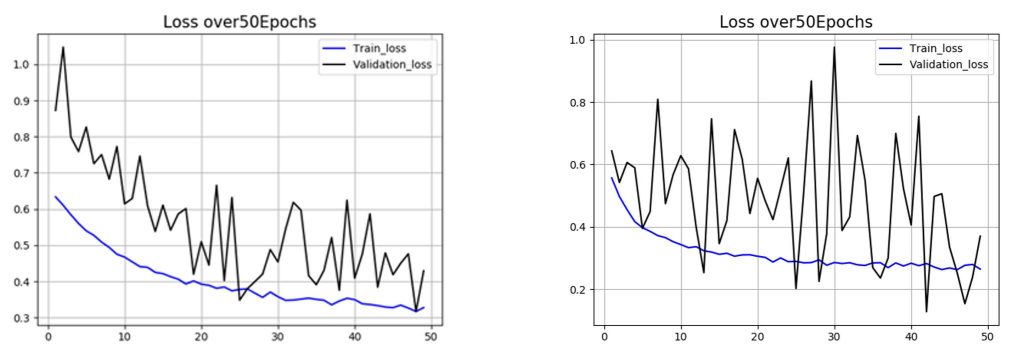
En parallèle de l’analyse de la précision, l’évolution de la perte au cours des 50 époques a permis de contrôler le processus d’apprentissage des différents modèles (Figure 6B). Le modèle ayant le moins d’unités possède une diminution de la perte pour les données de validation beaucoup plus stable que le modèle numéro 2.
Finalement, les valeurs des différentes précisions et pertes en fonction des deux modèles et des différents jeux de données ont été placées dans un tableau afin de les comparer (Figure 6C).
L’analyse de la variance repose sur la différence entre la précision sur le jeu d’entraînement et celle du jeu de validation. La variance du modèle 1 est supérieure à celle du modèle 2, respectivement 9,18% et 7,55%.
Et l’analyse du biais repose quant à elle sur l’analyse de la précision sur le jeu d’entraînement. Le modèle avec le moins d’unités possède une précision plus basse que le modèle 2, respectivement 90,27% et 88,42%.
Ce biais et variance plus élevés pour le modèle 1 se retrouvent lors de l’évaluation de la précision sur le jeu de test. La précision sur le jeu de test pour le modèle 1 est de 64,35% alors que pour le modèle 2, elle est de 74,13%.

Discussion
L’analyse de la précision et de la perte a permis de sélectionner 2 modèles de réseaux convolutifs. Un modèle avec 32 unités et un modèle avec 256 unités dans la couche cachée supplémentaire. L’augmentation du nombre d’unités a permis la diminution du biais et de la variance. La prédiction sur le jeu de données test était alors meilleure. Cependant, en comparant le tracé de la courbe d’évolution de la perte en fonction des époques pour le jeu de validation, on observe que l’augmentation du nombre d’unités entraîne une instabilité des valeurs de perte. Cette instabilité peu résulter d’une difficulté pour l’algorithme à converger vers le minimum de la fonction de coût.
Malgré des résultats prometteurs, la précision du CNN à 256 unités sur le jeu de test montre un biais et une variance encore trop élevés. Avec une précision de 74,13% et une variance de 7,55%
Afin d’optimiser cet algorithme, de nombreuses méthodes et réglages sont à notre disposition.
Biais élevé
Dans un premier temps, ce réseau convolutif présente un biais élevé. La modification de l’architecture du CNN est une des premières caractéristiques sur laquelle nous pouvons agir. Le nombre d’unités par couche cachée puis le nombre de couches du réseau pourraient être augmentés.
La bibliothèque keras possède également de nombreux modèles pré-entraînés. L’utilisation d’autres modèles comme VGG16 ou ResNet10 pourrait permettre une diminution du taux d’erreurs.
Variance élevée
Un sur-ajustement est observé sur nos données d’entraînement. Une des solutions serait de modifier les hyperparamètres lors de l’enrichissement des données.
Dans l’apprentissage profond, lorsque la variance est trop élevée, une autre méthode de régularisation est l’arrêt précoce « early stopping ». Cette technique permet de connaître le nombre d’itérations pouvant être exécuté avant que l’algorithme ne sur-ajuste.
Augmentation de la vitesse d’apprentissage
Comme nous gelons l’ensemble des couches, certaines fonctions sont fixes, car on ne les modifie pas. Pour accélérer l’entraînement, une des astuces serait de pré-calculer les caractéristiques de la dernière couche cachée du réseau pré-entraîné pour tous les exemples d’entraînement et de les sauver sur le disque dur. Cela éviterait de calculer les activations à chaque étape de l’entraînement.
Vérification du gradient
La propagation arrière est très délicate à mettre en œuvre. De nombreux bugs peuvent apparaître lors de l’implémentation. La diminution de la fonction de coût peut sembler correcte malgré ses bugs. La vérification de gradient serait une bonne astuce à utiliser pour vérifier si l’implémentation de la propagation arrière est correcte en vérifiant les dérivés.
Conclusion
La création d’un nouvel outil de vision par ordinateur aidant au diagnostic permettrait une diminution du taux de mortalité par pneumonie chez les enfants de 5 ans et moins. Dans cet article, la précision du réseau convolutif sur un faible jeu de données grâce à une méthode d’apprentissage par transfert n’est pas entièrement satisfaisante. Effectivement cet algorithme présente en moyenne 1 risque sur 4 de se tromper. L’objectif est donc de diminuer le biais, tout en évitant le sur-ajustement. Pour cela, de nombreuses méthodes peuvent être utilisées, comme l’augmentation du nombre d’unités ou le changement du modèle préformé. Le résultat final souhaité, se rapprocherait alors de l’erreur minimale souhaitée appelée « erreur de Bayes ». Dans notre cas, cette erreur est admise comme l’erreur minimale réalisée par un comité d’expert en radiologie.
Crédit de l’image de couverture : Kermany, Daniel; Zhang, Kang; Goldbaum, Michael (2018), “Labeled Optical Coherence Tomography (OCT) and Chest X-Ray Images for Classification”, Mendeley Data, v2 – CC BY 4.0

![Spark 3 : à la découverte des RDD [Part 2]](https://penseeartificielle.fr/wp-content/uploads/2022/02/fire-1905608_1280-218x150.jpg)
![Installation de Spark 3 sous Windows [Part 1]](https://penseeartificielle.fr/wp-content/uploads/2022/02/pexels-fabiano-rodrigues-1662298-218x150.jpg)
