Prérequis

Pour suivre et comprendre cet article dans les meilleurs conditions, il est recommandé de :

Introduction

Cet article est la deuxième partie des deux aricles sur lesquels on traite la regréssion linéaire avec une variable. Dans la première partie, on a pu représenter notre modèle et definit la fonction d’erreur. Dans cette seconde partie, nous allons entrainer notre modèle en utilisant la descente de gradient.
Pour ce faire, nous allons dans un premier temps voir ce qu’est la descente de gradient pour, ensuite, l’appliquer à notre modèle pour l’entrainement.

Rappel du code de la première partie

Nous reprennons ci-dessous, en guise de rappel, tous le code de la première partie de cette article

import numpy as np
tab = np.genfromtxt('food-truck_profits.txt', delimiter=',')

# recuperation des nombres d'habitants des villes
X = tab[:,0];

# recuperation des profits des food truck respectivement sur ces villes
Y = tab[:,1];

dataset = np.ones((np.size(X),2))
dataset[:,0] = X
dataset[:,1] = Y

# on affiche les 10 premiers food truck
print(dataset[0:9,:])

datasetTemp = dataset

dataset = np.ones((np.size(X),3))
dataset[:,1] = datasetTemp[:,0]
dataset[:,2] = datasetTemp[:,1]

X = dataset[:,0:2]
Y = dataset[:,2]

print(X.shape)
print(X)
print(Y.shape)
print(Y)


## Definition du modele
def h_theta(X, theta):
    ret = np.dot(theta, X.T)
    return ret

# pour theta = (0.5, 1)
theta = np.array([0.5, 1])

x = np.array([1, 6.1101])
print("pour theta = (0.5, 1), et x = (1, 6.1101) h_theta(x) vaut : ", h_theta(x,theta))

print("pour theta = (0.5, 1), et X est le dataset,  h_theta(x) vaut : ", h_theta(X,theta))


## Definition de la fonction d'erreur
def computeErrorFunction(x, y, theta):
    h_theta_de_x = h_theta(x,theta)
    vec_temp =  (h_theta_de_x - y)**2
    ret = np.sum(vec_temp)/(2*(y.size))
    return ret

theta = np.array([0.5, 1])
print("pour theta = (0.5, 1), l'erreur de notre modèle sur notre dataset est :", computeErrorFunction(X, Y, theta))

theta = np.array([12, 30])
print("pour theta = (500, 1000), l'erreur de notre modèle sur notre dataset est :", computeErrorFunction(X, Y, theta))

Entrainement du modèle

L’entrainement du modèle consiste à trouver le vecteur paramètre theta = (theta_0, theta_1) pour lequel la fonction d’erreur J(theta) est la plus proche de 0 possible. Pour ce faire, nous devons minimiser la fonction J(theta) :
 
\( \underset{\Theta_{0}, \Theta_{1}}{min}J(\Theta) \)
 

On minimise \( J(\Theta) \) en faisant une descente de gradient.

Descente de gradient 

La descente de gradient est un algorithme qui permet de trouver le minimum d’une focntion.
Si on veut trouver le minimum d’une fonction f(x) par exemple (\( \underset{x}{min}f(x) \)), calculer f(x) pour toutes les valeur possibles de x serait trés couteux en ressources informatique et en temps de calcul.
Il existe un meilleur outils (largement utilisé en machine learning) qui s’appelle la descente de gradient.
 
Les différentes étapes d’une descente de gradient sont : 
  1. La première etape de la descente de gradient est de choisir au hasard pour x une valeur \(x_0\) de départ.
  2. Ensuite, on calcule le gradient de la fonction f au point \(x_0\) (qui est \(f'(x_0)\)). 
    En effet, le gradient est un vecteur qui indique toujours la direction de la croissance 
    maximale de la fonction. Par exemple, le schéma suivant illustre cela :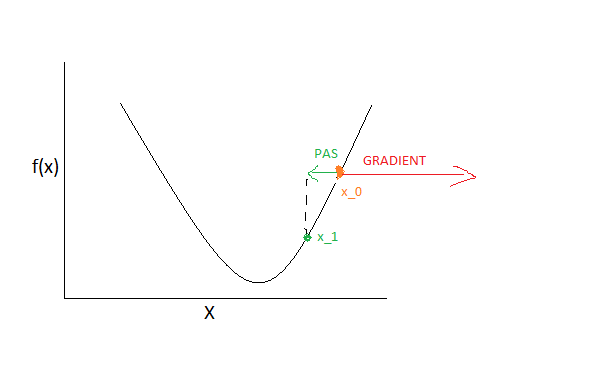
    Crédit : Mar Mbengue
  3. Comme le gradient indique la direction de la valeur maximale de la fonction, donc pour avoir 
    une nouvelle valeur de x qui nous permette de nous rapprocher de la valeur minimale de la fonction f(x) 
    on fait un pas vers la direction inverse du gradient. ce qui nous donne une nouvelle valeur \(x_1 = x_0 – \alpha*f'(x_0)\).
     
  4. repéter les etapes 1, 2, et 3 avec la nouvelle valeur \(x_1\) de x.
  5. En iterant plusieurs fois sur ce procédé, on va arriver à une valeur x_n tel que \( f(x_{n}) \approx 0\)
 
Et là, on dit qu’on a atteint notre point de convergence.
Crédit : Mar Mbengue – Tous droits réservés

\(\alpha\) est un paramètre de l’algorithme de descente de gradient. On l’appelle le pas d’apprentissage (learning rate en anglais). la valeur de alpha doit etre fixé avant le debut de la descente de grandient. Il ne doit être ni trop petit ni trop grand.

Application de la descente de gradient à notre modèle de regression linéaire

L’entrainement du modèle consiste à minimiser la fonction d’erreur : \(\underset{\Theta_{0}, \Theta_{1}}{min}J(\Theta)\).
 
Pour ce faire, nous allons appliqué la descente de gradient sur la fonction \(J(\Theta)\).
Dans le cas de notre fonction \(J(\Theta)\), on a deux inconnues \(\Theta_0\) et \(\Theta_1\). au lieu de calculer \(J'(\Theta)\), on calcule les dérivés partiels \(\frac{\partial}{\partial \Theta_0}J(\Theta) \hspace{0.2cm} et \hspace{0.2cm} \frac{\partial}{\partial \Theta_1}J(\Theta)\)
 
Ces dérivés partielles sont les suivants : 
 
\( \frac{\partial}{\partial \Theta_0}J(\Theta) = \frac{1}{m}\sum_{i=1}^{m}\left ( h_\Theta (x^{(i)}) – y^{(i)} \right ) \)
 
\( \frac{\partial}{\partial \Theta_1}J(\Theta) = \frac{1}{m}\sum_{i=1}^{m}(\left ( h_\Theta (x^{(i)}) – y^{(i)} \right )x^{(i)}_1) \)
 
Dabord, on choisit des valeurs initiaux (au hasarrd) pour \(\Theta_0\) et \(\Theta_1\)
 
Ensuite, on fait les itérations : 
repeter {
\( \Theta_0 := \Theta_0 – \alpha \frac{1}{m}\sum_{i=1}^{m}\left ( h_\Theta (x^{(i)}) – y^{(i)} \right ) \)
\( \Theta_1 := \Theta_1 – \alpha \frac{1}{m}\sum_{i=1}^{m}(\left ( h_\Theta (x^{(i)}) – y^{(i)} \right )x^{(i)}_1) \)
}
 
En machine learning, chaque itération est appelé époque. le nombre d’époques est un paramètre de l’apprentissage.
Pour implémenter véctoriellement l’entrainement de notre modèle, On transforme les paramtres theta et les gradients (dérivés partielles) en vecteur \( \Theta =\begin{pmatrix} {\Theta_0}\\ {\Theta_1} \end{pmatrix} \hspace{0.2cm} et \hspace{0.2cm} \nabla J(\Theta ) = \begin{pmatrix}{\frac{\partial}{\partial \Theta_0}J(\Theta)}\\{\frac{\partial}{\partial \Theta_1}J(\Theta)}\end{pmatrix}\)
Notre itération devient :  
repeter {
\( \Theta := \Theta \hspace{0.2cm} – \alpha \hspace{0.1cm} \nabla J(\Theta ) \)
}
 

Ainsi, on implémente la fonction python qui calcule les gradients et qui recoit en paramètre les éléments suivants: 

  • une matrice mx2 ou un vecteur
  • un vecteur theta
  • un vecteur Y

cette fonction va retourner le vercteur de gradient \( \nabla J(\Theta ) \).

def computeGradient(x, y, theta):
    h_theta_de_x = h_theta(x,theta)
    vec_temp =  (h_theta_de_x - y)
    ret = np.dot(x.T,vec_temp)/y.size
    return ret
Nous pouvons donc calculer le vecteur des gradients pour voir ce que celà donne :
theta = np.array([0.5, 1])
print("pour theta = (0.5, 1), le vecteur des gradients est :", computeGradient(X, Y, theta))
pour theta = (0.5, 1), le vecteur des gradients est : [ 2.82066495 20.15499308]
 
On peut aussi implémenter la fonction python qui entraine notre modèle. Cette fonction prend en paramètres : 
  • un vecteur une matrice mx2
  • un vecteur Y
  • le nombre d’époques
  • le learning rate (alpha)
la fonction va retourner le vecteur de theta pour lequel notre fonction d’erreur sera minimum.
np.seterr(all='warn')
np.set_printoptions(suppress=True)
def trainModel(x, y, nb_epoch, alpha=0.01):
    # on choisi des valeurs arbitraires pour le vecteur theta
    theta = np.array([0.5, 1])
    # on itere sur le nombre d'epoques
    for i in range(nb_epoch):
        grad = computeGradient(x, y, theta)
        theta = theta - alpha*grad
        if i == 15 : 
            print("theta ", theta)
            print("gradient :", grad)
            print("h_theta : ",h_theta(x,theta))
            
        print("Epoque ", i)
        print("l'erreur est : ", "%.5f"%computeErrorFunction(x, y, theta))
    
    return theta

 

Entrainons notre modèle (sur 1500 époques par exemple) en éxecutant le code suivant :

theta_train = trainModel(X, Y, 1500, 0.01)

Aprés l’entrainement, nous avons trouvé le vecteur theta suivant : 

print(theta_train)

Ce qui nous retourne : 

[-3.60387633  1.16370867]

Pour prédire le profit d’un nouveau food truck sur une ville de 1000 habitants, on fera :

x = np.array([1, 1000])
profit = h_theta(x,theta_train)
print("Pour une ville de 1000 habitants, le profit est estimé à : ","%.2f"%profit,"$")

résultat : 

Pour une ville de 1000 habitants, le profit est estimé à :  1160.10 $

Conclusion

Aprés avoir expliqué en détails l’algorithme de descente de gradient, nous l’avons appliqué 
à notre modèle. Ce qui nous a permis de trouver les meilleurs paramètres theta pour celui-ci. 
Cependant, il existe un autre moyen pour trouver les meillieures paramètres theta: c’est l’équation normale 
dont nous allons parlé dans les articles à venir.
 
Crédit de l’image de couverture : Sewaqu, Public domain, via Wikimedia Commons

ARTICLES CONNEXESPLUS DE L'AUTEUR