Prérequis
Pour suivre et comprendre cet article dans les meilleurs conditions, il est recommandé de :
- Lire l’article précédent (si ce n’est pas encore fait) qui est intitulé Introduction au machine Learning.
- Télécharger le dataset qui est disponible ici.
Introduction
Cet article est la première partie des deux articles dans lesquels on traite de la régression linéaire avec une variable. La régression linéaire fait partie de la catégorie des techniques d’apprentissage supervisé. Dans cet article, nous commencerons par parler du dataset (le comprendre et l’explorer) avant de représenter notre modèle pour ainsi terminer par la l’implémentation de la fonction d’erreur.
Comprendre le dataset
Nous allons réaliser un modèle qui permet de prédire le profit d’un food-truck à partir du nombre d’habitants de la ville où il sera stationné. Pour ce faire, nous disposons d’un dataset qui contient les profits de plusieurs food-truck stationnés dans plusieurs villes.
Le dataset a été téléchargé depuis Coursera. Il s’agit d’un fichier csv(food-truck_profits.txt) qui contient deux champs qui portent sur les profits de différents food truck dans des villes. Chaque ligne représente un food truck dans une ville.
Les deux champs sont :
- Le premier champ représente le nombre d’habitant de la ville.
-
Le deuxième champ représente le profit (en dollars) d’un food truck sur cette ville.
import numpy as np
tab = np.genfromtxt('food-truck_profits.txt', delimiter=',')
# recuperation des nombres d'habitants des villes
X = tab[:,0];
# recuperation des profits des food truck respectivement sur ces villes
Y = tab[:,1];
dataset = np.ones((np.size(X),2))
dataset[:,0] = X
dataset[:,1] = Y
# on affiche les 10 premiers food truck
print(dataset[0:9,:])
Ce qui nous donne le résultat suivant :
[[ 6.1101 17.592 ] [ 5.5277 9.1302] [ 8.5186 13.662 ] [ 7.0032 11.854 ] [ 5.8598 6.8233] [ 8.3829 11.886 ] [ 7.4764 4.3483] [ 8.5781 12. ] [ 6.4862 6.5987]]
On a recupéré le nombre d’habitants des villes (X) et le profit des food truck correspondant (Y) qu’on a mis sur un tableau à deux colonnes qui se nomme « dataset ».
On nomme m le nombre d’exemples (de food trucks) dans le dataset.On obtient ainsi l’ensemble \(E_m = \{(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),…,(x^{(m)},y^{(m)})\} \)
De ce fait \( (x^{(i)}, y^{(i)}) \) représente la i-ème ligne de la table « dataset » : le nombre d’habitant \( x^{(i)} \) de la i-ème ville et le profits \( y^{(i)} \) de la i-ème food truck dans cette ville.
Si on visualise le dataset, on aura :
import matplotlib.pyplot as plt plt.plot(dataset[:,0], dataset[:,1], 'rx') plt.show()
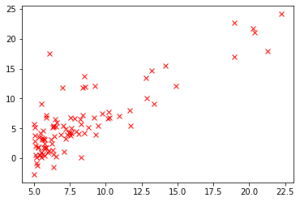
Représenter le modèle
Représentation du modèle
Nous avons maintenant notre dataset qui représente les profits des food truck en sachant le nombre d’habitants des villes qui les accueillent. Pour realiser le modele de régression linéaire, il nous faut trouver (apprendre) une fonction \( h_\Theta : X \rightarrow Y \)
Cette fonction est appelé \( h_\Theta \) par convention (h pour se reférer au mot « hypothese » et \( \Theta \) pour faire référence aux paramètres de la fonction).
Puisqu’il s’agit d’une regression linéaire, la fonction \( h_\Theta \) sera linéaire et elle sera représentée par :
\( h_\Theta (x) = \Theta_0 + \Theta_1 x \)
Pour que notre modèle soit pertinent, la condition suivante doit être vraie :
quelque soit \( (x^{(i)}, y^{(i)}) \in E_m \) , on a : \( h_\Theta (x^{(i)}) \approx y^{(i)} \).
Pour que la condition ci-dessus soit vraie, il nous faut trouver des valeurs adéquates pour les paramètres (\( \Theta_0 \) et \( \Theta_1 \)) de la fonction \( h_\Theta \).
Maintenant, la question qu’on peut se poser est « comment trouver les bonnes valeurs pour les paramètres \( \Theta_0 \) et \( \Theta_1 \) ? ». Nous allons y répondre dans la deuxième partie de cette article.
Implémentation vectorielle du modèle
Pour rendre notre fonction \( h_\Theta \). plus performante en temps de calcule, on peut le vectoriser. Selon wikipedia, « La vectorisation est le processus de conversion d’un programme informatique à partir d’une implémentation scalaire, qui traite une seule paire d’opérandes à la fois, à une implémentation vectorielle qui traite une opération sur plusieurs paires d’opérandes à la fois. »
Pour implémenter véctoriellement notre modèle :
- On transforme d’abord les parametres \( \Theta_0 \) et \( \Theta_1 \) en vecteur \( \Theta = \begin{pmatrix}{\Theta_0}\\ {\Theta_1}\end{pmatrix} \).
-
Ensuite, on transforme x en vecteur \( x =\begin{pmatrix}{x_0}\\ {x_1}\end{pmatrix} \) avec \( x_0=1 \) et \( x_1= nombre \hspace{0.2cm} d’habitants \).
La fonction \( h_\Theta \) devient alors :
\( h_\Theta (x) = \Theta^T x \)
Dans le reste de l’article et de la série, on implémentera toujours les modèles de manière vectorielle.
L’ensemble X des nombres d’habitants des villes va devenir : \( X = \begin{pmatrix} 1 & x^{(1)}_1\\ 1 & x^{(2)}_1\\ .&. \\ .&. \\ .&. \\ 1 & x^{(n)}_1\end{pmatrix} \)
Quand on fait une régréssion linéaire; on ajoute toujours (par convention) au debut du dataset une colonne dont toutes les valeurs sont égales à 1.
on modifie la varable dataset afin d’ajouter une colonne (avec des 1) devant. ce qui va nous donner :
datasetTemp = dataset dataset = np.ones((np.size(X),3)) dataset[:,1] = datasetTemp[:,0] dataset[:,2] = datasetTemp[:,1] X = dataset[:,0:2] Y = dataset[:,2] print(X.shape) print(X) print(Y.shape) print(Y)
Le résultat va ressembler à :
(97, 2)
[[ 1. 6.1101]
[ 1. 5.5277]
[ 1. 8.5186]
[ 1. 7.0032]
[ 1. 5.8598]
[ 1. 8.3829]
[ 1. 7.4764]
[ 1. 8.5781]
.
.
. ]
(97,)
[17.592 9.1302 13.662 11.854 6.8233 11.886 4.3483 12.
6.5987 3.8166 3.2522 15.505 3.1551 7.2258 0.71618 3.5129
5.3048 0.56077 3.6518 5.3893 3.1386 21.767 4.263 . . .]
On peut ainsi implémenter la fonction python qui correspond à \(h_\Theta \). Cette fonction prend en paramètres deux vecteurs :
- x (ou une matrice mx2).
-
\(\Theta \) correspondant aux paramètres de notre modèle.
On définit la fonction python qui représente notre modèle de la manière suivante :
def h_theta(X, theta):
ret = np.dot(theta, X.T)
return ret
# pour theta = (0.5, 1)
theta = np.array([0.5, 1])
x = np.array([1, 6.1101])
print("pour theta = (0.5, 1), et x = (1, 6.1101) h_theta(x) vaut : ", h_theta(x,theta))
print("pour theta = (0.5, 1), et X est le dataset, h_theta(x) vaut : ", h_theta(X,theta))
résultat :
pour theta = (0.5, 1), et x = (1, 6.1101) h_theta(x) vaut : 6.6101 pour theta = (0.5, 1), et X est le dataset, h_theta(x) vaut : [ 6.6101 6.0277 9.0186 7.5032 6.3598 8.8829 7.9764 9.0781 6.9862 5.5546 6.2107 14.664 6.234 8.9084 6.1407 5.8794 6.8654 5.6301 6.9296 7.5708 6.6891 20.77 5.9901 6.8261 6.0649 19.445 13.328 11.457 13.676 22.703 5.7524 7.0894 9.7482 6.3918 8.7111 8.4334 8.5959 6.1063 13.336 6.8534 5.9069 7.3825 12.208 6.2737 8.3247 7.5931 5.5702 6.3014 12.2 6.0416 8.0402 5.8077 7.9239 8.1031 6.8328 6.8589 6.7742 6.1397 9.8102 9.9536 9.3254 5.6793 21.779 15.408 19.459 7.7182 8.7951 10.736 5.9994 20.841 10.636 7.8345 6.5062 7.7259 5.5269 7.0479 8.0386 5.5365 10.774 5.6077 6.2292 5.6884 6.8557 10.2687 7.0159 9.0172 9.6802 6.502 6.0204 5.5594 6.2077 8.1366 6.3707 5.8054 8.7934 13.894 5.9369]
On voit que pour le premier exemple (food truck), la nombre d’habitants de la ville est 6.1101 et le profit est 17.592.
Quand on se sert de notre modèle h_theta pour estimer le profit de ce food truck on trouve 6.6101, ce qui veut dire que notre modèle n’est pas encore au point.
Pour qu’il soit au point il faudra l’entrainer avec notre dataset.
Fonction d’erreur
On a vu que notre modèle fait des erreurs dans l’estimation des profits des food truck. En prenant l’exemple du premier food truck de notre dataset qui est 17.592, notre modèle l’estime à 6.1101.
Ce qui représente une grosse erreur car le profit estimé par notre modèle est trés loin du profit réel.
On peut ainsi définir la fonction d’erreur comme la moyene des erreurs de notre modèle sur le dataset E_m, Ce qui nous donne :
\( J(\Theta ) = \frac{1}{2m}\sum_{i=1}^{m}(h_\Theta (x^{(i)}) – y^{(i)})^2 \)
Cette fonction est aussi appelé erreur quadratique.
Lors de l’entrainement du modèle, c’est cette fonction \( J(\Theta )\) qu’on va essayé de minimiser. Ce qui revient à trouver un vecteur de paramèttre \( \Theta = \begin{pmatrix}{\Theta_0}\\ {\Theta_1}\end{pmatrix} \) pour lequel \( J(\Theta )\) serait le plus proche de 0.
On peut ainsi implémenter la fonction python qui correspond à la fonction d’erreur \( J(\Theta )\).
Cette fonction prend en parametre :
- x (vecteur ou matrice mx2).
- Un vecteur theta.
- Un vecteur Y (ou un scalaire \(y_i\)).
et retourne la valeur de \( J(\Theta )\).
def computeErrorFunction(x, y, theta):
h_theta_de_x = h_theta(x,theta)
vec_temp = (h_theta_de_x - y)**2
ret = np.sum(vec_temp)/(2*(y.size))
return ret
on peut calculer l’erreur :
theta = np.array([0.5, 1])
print("pour theta = (0.5, 1), l'erreur de notre modèle sur notre dataset est :", computeErrorFunction(X, Y, theta))
theta = np.array([12, 30])
print("pour theta = (500, 1000), l'erreur de notre modèle sur notre dataset est :", computeErrorFunction(X, Y, theta))
résultat :
pour theta = (0.5, 1), l'erreur de notre modèle sur notre dataset est : 8.731188017156702 pour theta = (500, 1000), l'erreur de notre modèle sur notre dataset est : 37643.43989082003
On voit que l’erreur est plus petite avec theta = (0.5, 1) qu’avec theta = (500, 1000), donc notre modèle est plus performant avec le parametre theta = (0.5, 1).
Conclusion
Aprés avoir définit la fonction d’erreurs, exploré le dataset et donner une représentation de notre modèle, on peut dire que notre modèle n’est pas encore performant car n’ayant pas les bons paramètres. Pour retrouver les bons paramètres, il faudra entrainer le modèle. D’ou l’objet de la deuxième partie de cet article qui va porter sur l’entrainement d’un modèle.
Crédit de l’image de couverture : Chire – CC BY-SA 3.0

![Spark 3 : à la découverte des RDD [Part 2]](https://penseeartificielle.fr/wp-content/uploads/2022/02/fire-1905608_1280-218x150.jpg)
![Installation de Spark 3 sous Windows [Part 1]](https://penseeartificielle.fr/wp-content/uploads/2022/02/pexels-fabiano-rodrigues-1662298-218x150.jpg)
