Prérequis
Pour suivre et comprendre cet article dans les meilleurs conditions, il est recommandé de :
- Lire le premier article de la série (si ce n’est pas encore fait) qui est intitulé Introduction au machine Learning.
- Télécharger le dataset qui est disponible ici.
Introduction
Exploration des données
Le dataset a été téléchargé depuis Coursera. Il s’agit d’un fichier csv (houses-pricing.txt) qui contient trois champs qui portent sur les différentes maisons (Chaque ligne représente une maison).
Les trois champs sont :
- Le premier champ représente la surface de la maison en metre carré.
- Le deuxième champ représente le nombre de chambres de la maison.
- Le troisième champ représente le prix de la maison en (1000$)
Maintenant, récupérons le dataset pour voir à quoi ils ressemblent.
import numpy as np
tab = np.genfromtxt('houses-pricing.txt', delimiter=',')
# recuperation des surfaces des maisons
x1 = tab[:,0];
# recuperation des nombres de chambres pour chaque maisons
x2 = tab[:,1];
# recuperation des prix des maisons
Y = tab[:,2];
dataset = np.ones((np.size(x1),3))
dataset[:,0] = x1
dataset[:,1] = x2
dataset[:,2] = Y
# on affiche les 10 premiers maisons
print(dataset[0:9,:])
On aura comme résultat :
[[2.10400e+03 3.00000e+00 3.99900e+05] [1.60000e+03 3.00000e+00 3.29900e+05] [2.40000e+03 3.00000e+00 3.69000e+05] [1.41600e+03 2.00000e+00 2.32000e+05] [3.00000e+03 4.00000e+00 5.39900e+05] [1.98500e+03 4.00000e+00 2.99900e+05] [1.53400e+03 3.00000e+00 3.14900e+05] [1.42700e+03 3.00000e+00 1.98999e+05] [1.38000e+03 3.00000e+00 2.12000e+05]]
On a recupéré les surfaces des maisons (x1), les nombres de chambres pour chaque maisons (x2) et les prix des maisons correspondantes (Y) qu’on a mis sur un tableau à trois colonnes qui se nomme “dataset”.
On nomme m le nombre d’exemples (de maisons) dans le dataset. On obtient ainsi l’ensemble :
\(E_m = \{(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),…,(x^{(m)},y^{(m)})\} \) \( avec \: \: \: \: x^{(i)}=\begin{pmatrix} x^{(i)}_{1}\\ x^{(i)}_{2} \end{pmatrix} \: \forall \: 0 < i \leq m \)De ce fait \( (x^{(i)},y^{(i)}) \) représente la i-ème ligne de la table “dataset” :
- la surface \( x^{(i)}_1 \) de la i-ème maison
- le nombre de chambres \( x^{(i)}_2 \) de la i-ème maison
- et le prix \( y^{(i)} \) de la i-ème maison.
Ici, X est un vecteur de dimension 2 contrairement à l’article précédent ou X était un sacalaire. ce qui veut dire qu’on fait une régréssion avec 2 variables.
Si on représente vectoriellement tout le dataset, on aura :
\( \forall \: x^{(i)} \in \: X, \: on \: aura \: \: x^{(i)}=\begin{pmatrix} x^{(i)}_{0}\\ x^{(i)}_{1}\\ x^{(i)}_{2} \end{pmatrix} \: avec \: x^{(i)}_{0} = 1 \)L’ensemble X va devenir alors : \( X = \begin{pmatrix} 1 & x^{(1)}_{1} & x^{(1)}_{2}\\ 1 & x^{(2)}_{1} & x^{(2)}_{2}\\ . & . & .\\ . & . & .\\ 1 & x^{(m)}_{1} & x^{(m)}_{2} \end{pmatrix} \)
On modifie la varable dataset afin d’ajouter une colonne (avec des 1) devant, ce qui va nous donner :
datasetTemp = dataset dataset = np.ones((np.size(x1),4)) dataset[:,1] = datasetTemp[:,0] dataset[:,2] = datasetTemp[:,1] dataset[:,3] = datasetTemp[:,2] X = dataset[:,0:3] Y = dataset[:,3] print(X.shape) print(X) print(Y.shape) print(Y)
Représentation du modèle et de la fonction d’erreur
Représentation du modèle
Pour realiser le modele de régression linéaire, il nous faut trouver (apprendre) une fonction
\( h_{\Theta} : X \rightarrow Y \)
D’une manière plus générale, la fonction hypothèse d’une régression lineaire avec plusieurs variables (Multivariate regression) est :
\( x^{(i)} \, \, represente \, une \, maison \, avec \\ x^{(i)}_{0} = 1;\\ x^{(i)}_{1} = surface \, de \, la \, maison \, (en \, m^{2});\\ x^{(i)}_{2} = nombre \, de \, chambres \, de \, la \, maison. \)
On peut ainsi implémenter la fonction python qui correspond à hΘ. Cette fonction prend en paramètres deux vecteurs :
- x (ou une matrice mx3).
- Θ correspondant aux paramètres de notre modèle.
def h_theta(X, theta):
ret = np.dot(theta, X.T)
return ret
voyons ce que donne la fonction h_theta sur notre dataset :
# pour theta = (0.5, 1, 2)
theta = np.array([0.5, 1, 2])
x = np.array([1, 2104, 3])
print("pour theta = (0.5, 1, 2), et x = (1, 2104, 3) h_theta(x) vaut : ", h_theta(x,theta))
print("pour theta = (0.5, 1, 2), et X est le dataset, h_theta(x) vaut : ", h_theta(X,theta))
résultat :
pour theta = (0.5, 1, 2), et x = (1, 2104, 3) h_theta(x) vaut : 2110.5 pour theta = (0.5, 1, 2), et X est le dataset, h_theta(x) vaut : [2110.5 1606.5 2406.5 1420.5 3008.5 1993.5 1540.5 1433.5 1386.5 1500.5 1948.5 2006.5 1896.5 4488.5 1274.5 2308.5 1324.5 1242.5 2617.5 3039.5 1773.5 1892.5 1610.5 1970.5 3896.5 1106.5 1464.5 2532.5 2206.5 2643.5 1843.5 1002.5 2048.5 3143.5 1819.5 1443.5 1245.5 2140.5 4223.5 2170.5 1668.5 2244.5 2575.5 1206.5 856.5 1860.5 1209.5]
On voit que pour le premier exemple (maison), la surface de la maison est 2104, le nombre de cahmbres est 3, et le prix 399900. Si on utilise notre modèle h_theta pour estimer le prix de cette maison on trouve 2110.5, ce qui veut dire que notre modèle n’est pas encore performant.
Représentation de la fonction d’erreur
On peut ainsi implémenter la fonction python qui correspond à la fonction d’erreur J(Θ). Cette fonction prend en paramètres deux vecteurs :
- x (ou une matrice mx3).
- Θ correspondant aux paramètres de notre modèle.
- Un vecteur Y (ou un scalaire yi).
def computeErrorFunction(x, y, theta):
h_theta_de_x = h_theta(x,theta)
vec_temp = (h_theta_de_x - y)**2
ret = np.sum(vec_temp)/(2*(y.size))
return ret
On peut calculer l’erreur :
theta = np.array([0.5, 1, 2])
print("pour theta = (0.5, 1, 2), l'erreur de notre modèle sur notre dataset est :", computeErrorFunction(X, Y, theta))
theta = np.array([1200, 30000, 45000])
print("pour theta = (1200, 300, 450), l'erreur de notre modèle sur notre dataset est :", computeErrorFunction(X, Y, theta))
Résultat :
pour theta = (0.5, 1, 2), l'erreur de notre modèle sur notre dataset est : 64827252828.65691 pour theta = (1200, 300, 450), l'erreur de notre modèle sur notre dataset est : 2065558659029510.2
Entrainement du modèle
Descente de gradient
Si nous avons un modèle de regression de n variables alors nous avons n+1 paramètres theta. L’entrainement du modèle consistera à minimiser la fonction d’erreur
\( \underset{\Theta_{0}, \Theta_{1},…,\Theta_{n+1}}{min}J(\Theta) \)
Ce qui reviendrait à faire le traitement suivant :
répéter {
Sachant que les dérivés partielles par rapport au différents paramètres sont les suivants :
Ainsi, on implémente la fonction python qui calcule les gradients et qui recoit en paramètre les éléments suivants:
- une matrice mx3.
- Θ correspondant aux paramètres de notre modèle.
- Un vecteur Y (ou un scalaire yi).
Cette fonction va retourner le vercteur de gradient \( \nabla J(\Theta ) \)
def computeGradient(x, y, theta):
h_theta_de_x = h_theta(x,theta)
vec_temp = (h_theta_de_x - y)
ret = np.dot(x.T,vec_temp)/y.size
return ret
Nous pouvons donc calculer le vecteur des gradients pour voir ce que celà donne :
theta = np.array([0.5, 1, 2])
print("pour theta = (0.5, 1), le vecteur des gradients est :", computeGradient(X, Y, theta))
Résultat :
pour theta = (0.5, 1), le vecteur des gradients est : [-3.38405138e+05 -7.59573941e+08 -1.11367086e+06]
A l’image de la fonction de calcul de gradient, la fontion d’entrainement du modèle est pareil que pour une régression linéaire avec une seule variable. La fonction sera défini ainsi :
import matplotlib.pyplot as plt
np.seterr(all='warn')
np.set_printoptions(suppress=True)
def trainModel(x, y, nb_epoch, alpha=0.01):
# on choisi des valeurs arbitraires pour le vecteur theta
theta = np.random.rand(3)
scem = np.zeros((nb_epoch//1000, 2))
print("theta ", theta)
# on itere sur le nombre d'epoques
for i in range(nb_epoch+1):
grad = computeGradient(x, y, theta)
theta = theta - alpha*grad
if i%1000 == 0 :
err = computeErrorFunction(x, y, theta)
print("theta ", theta)
print("gradient :", grad)
print("h_theta : ",h_theta(x,theta))
print("Epoque ", i)
print("l'erreur est : ", err)
l = (i//1000) - 1
scem[l, 0] = i
scem[l, 1] = err
print(scem)
plt.plot(scem[:,0], scem[:,1], linestyle='solid')
plt.show()
return theta
Entrainons notre modèle (sur 2000 époques par exemple) en éxecutant le code suivant :
theta_train = trainModel(X, Y, 15000, 0.01)
Normalisation
Nous avons l’impression que l’erreur augmente au fure et à mesure que l’entrainement avance alors que ca devrai etre le contraire.
- \( \text{la surface $ x_{1}^{(i)} $ est de tel sorte que $ 852 \leq x_{1}^{(i)}\leq 4478 $} \)
- \( \text{le nombre de chambres $ x_{2}^{(i)} $ est de tel sorte que $ 1 \leq x_{2}^{(i)}\leq 5 $} \)
Lors d’une regression lineaire avec plusieurs varables, pour que descente de gradient se passe bien, il faut que tous les caracteristiques (variables) aient des valeurs dans le meme echelle; cela signifie que :
mu = np.zeros(np.size(X, 1))
s = np.zeros(np.size(X, 1))
mu = np.mean(X, axis=0, dtype=int)
min = np.min(X, axis=0)
max = np.max(X, axis=0)
s = max - min
def normalize(X, mu, s):
X_norm = X
for i in range(np.size(X_norm,0)) :
X_norm[i,:] = X_norm[i,:] - mu
for j in range(np.size(X_norm,1)) :
X_norm[i,j] = X_norm[i,j]/s[j]
# nous remettons les 1 à leurs places
X_norm[:,0] = np.ones(np.size(X_norm,0),dtype=int)
return X_norm
X_norm = normalize(X, mu, s)
theta_train = trainModel(X_norm, Y, 15000, 0.01)
Regréssion polynomiale
Lorsqu’on effectue une régression lineaire, il peut arriver que le modèle linéaire qu’on a appris ne puisse pas pemettre de faire les prédiction attendu.
En visualisant les données, on se rend compte que l’affichage des données prend la forme d’une courbe au lieu d’une droite. sachant qu’une fonction linéaire ne peut représenter qu’une droite; un modeèle linéaire ne peut pas apprendre nos données correctement (c’est ce qui explique les disfonctionnements de notre modèle)
Pour apprendre un modèle à partir de ces données (sous forme de courbe), il nous faut faire une regréssion polynomiale en lieu et place de la regréssion linéaire.
La régression polynomiale consiste à modifier fonction linéaire en fonction polynamiale en créant de nouvelle caractéristiques à partie des caractéristiquers existants. cette modification (transfomation) nous donnera une fonction quadratique, cubique, racine carrée, etc.
Par exemple, supposons qu’on ait le modèle de regréssion suivant :
Nous pouvons créer des caractéristiques additionnelles à partir de x. Pour avoir la fonction quadratique, on fait :
Equation normale
La descente de gradient est un moyen de minimiser le fonction d’erreur J_theta. Cependant, il existe une seconde manière de minimiser la fonction d’erreur. cette manière de faire est appelé Equation Normale. Cette manière de faire permet d’effectuer la minimisation explicitement et sans recourir à un algorithme itératif. Dans la méthode « Équation normale », nous minimiserons J en prenant explicitement ses dérivés par rapport aux θj, et en les mettant à zéro. Cela nous permet de trouver le thêta optimal sans itération. La formule d’équation normale est donnée ci-dessous :
- X est une matrice mxn qui est composé par l’ensemble des exemples d’entrainement sans les target : dans notre cas, chaque ligne représente un maison.
- y est un vecteur de dimension m qui représente l’ensemble des target : chaque élément de ce vecteur représente le prix d’une maison.
Nous pouvons définir la fonction qui calcule theta en utilisant l’equation normale. cette fonction va recevoir les paramètres suivants :
- une matrice mx3.
- Un vecteur y.
def equationNormale(X, y):
matM = np.dot(X.T, X)
matInv = np.linalg.inv(matM)
mat = np.dot(matInv, X.T)
theta = np.dot(mat, y)
return theta
theta = equationNormale(X, Y) print(theta)
Résultat :
[341805.20024107 504777.90398791 -34952.07644931]
Avec l’equation Normale, on a pas besoin de choisir un learning rate ni de faire plusieurs itération comme on le ferait sur un descente de gradient.
Par contre, si on a un nombre de feature trés grand (>10000), faire une descente de gradient ira beaucoup plus vite que de calculer l’équation normale. En plus, l’equation normale ne fonctionne que pour la regréssion linéaire mais pas pour les autres algorithme plus complexes (classification, regression logistique, reseau de neurone, etc.).
Conclusion
Aprés avoir explorer notre dataset, réprésenter notre modèle (ainsi que sa fonction d’erreur), nous avons entrainer notre modèle en utilisant une descente de gradient.
Dans cette article, nous avons aussi expliquer ce qui est la normalisation ainsi que son utilité dans l’apprentissage d’un modèle; Nous avons aussi montré un autre moyen de trouver les paramètres du modèle (Equation noemale).
Nous allons parler de classification avec regression logistique dans le prochain article de la série.
Crédit de l’image de couverture : Mar Mbengue

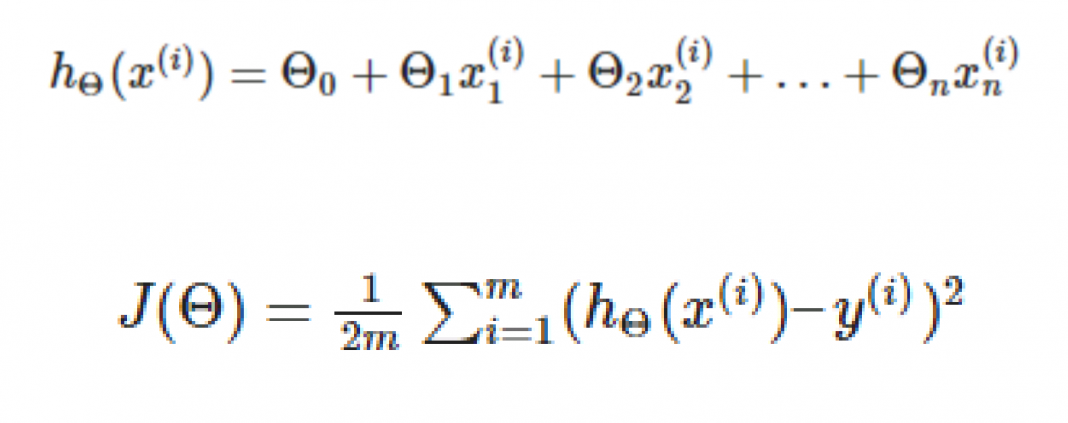
![Spark 3 : à la découverte des RDD [Part 2]](https://penseeartificielle.fr/wp-content/uploads/2022/02/fire-1905608_1280-218x150.jpg)
![Installation de Spark 3 sous Windows [Part 1]](https://penseeartificielle.fr/wp-content/uploads/2022/02/pexels-fabiano-rodrigues-1662298-218x150.jpg)
