Bonjour à tous,
Dans cet article nous allons voir les CSPs qui font l’objet de nombreuses recherche en intelligence artificielle.
Tout d’abord nous allons expliquer le principe du sudoku puis nous décrirons les CSP de manière la plus simple et la plus compréhensible qui soit. En tout cas je l’espère … en outre nous irons à la découverte du théorème des quatre couleurs puis pour finir nous allons explorer les possibilités qu’offrent les CSPs
Le principe du sudoku
Le sudoku est un jeu individuel qui consiste à compléter une grille de « sudoku ». La grille est composé de :
- 9 lignes
- 9 colonnes
- 9 carrés
Le sudoku ne doit jamais avoir un ou plusieurs chiffre(s) identique dans la même colonne, la même ligne ou dans le même carré. Un carré est un total de 9 cases donc il y a 9 carrés dans le sudoku. Avant de commencer le sudoku, certaines cases de la grille sont déjà complété aléatoirement selon des règles.

En raison de la patience et de l’expérience de la personne il existe plusieurs difficultés.
Voici les différentes catégories :
- Facile (pour commencer)
- Moyen
- Difficile
- Diabolique (pour les experts)
Sudoku à solution unique
Le sudoku fait partie des jeux à n’avoir qu’une seule et unique solution possible. Il n’existe pas de sudoku aillant plusieurs solution. À vous de la trouver.
Le nombre de grille complètes possibles est de 6,67.10^21
D’après Bertram Felgenhauer et Frazer Jarvis
Cependant, plusieurs grilles sont équivalentes si on prend en compte un certain nombre de symétries (exemple : échange des lignes avec les colonnes, permutations des 9 nombres …)
Au final il y a 5 472 730 538 grilles non équivalentes
D’après Jarvis et Russell
En conséquence il est presque impossible de tomber sur deux grilles identique. Il serait intéressante de concevoir un algorithme capable de résoudre les sudokus en très peu de temps.
Les CSP
Tout d’abord CSP est l’abréviation de Constraint Satisfaction Problem qui se traduit en français par les problème de satisfaction de contraintes. La programmation par contraintes sert à résoudre certains problèmes combinatoires de grandes tailles. Ce sont des problèmes mathématiques utilisés en intelligence artificielle et en recherche opérationnelle.
La définition formelle
Formellement les CSP s’expriment selon trois variables dans un triplet <X, D, C> où
– X est un ensemble n de variables.
– D est un ensemble de n domaines de valeurs.
– C est un ensemble de contrainte.
Application théorique du Sudoku
Dans la théorie le triplet du Sudoku est défini comme suit :
– X est l’ensemble des cases de la grille
– D est l’ensemble des valeurs que peut prendre une variable
– C est l’ensemble des contraintes défini dans le Sudoku donc on cherche que toute les variables de la même ligne, de la même colonne et du même carré soit différent.
Application pratique du Sudoku
Dans la pratique les variables sont défini comme suit :
– X vaut [x0, x2, x3, …., x9,
x10, x11, ….., x19,
…….., ….
x72, x73, …., x81]
– D vaut [1, 2, 3, 4, 5, 6, 7, 8, 9]
– C est une fonction défini comme suit
[X[0], X[1], X[2], X[3], X[4], X[5], X[6], X[7], X[8]
……, ………, …….., ………, ………, ………, ……., ……….
X[72], X[73], X[74], X[75], X[76], X[77], X[78], X[79], X[80]]
Voilà pour la résolution de Sudoku. Dans cette partie nous avons défini la résolution des Sudokus grâce au CSP. Maintenant nous allons voir un autre problème abordé par la programmation par contraintes. Ce problème étant d’attribuer des couleurs différentes à chaque états de l’Australie.
Pseudo-code du Sudoku
Ci-dessous un exemple de pseudo-code pour la vérification de Sudoku.
Fonction main()
Pour i = 11 de 0 jusqu'à 91 avec un pas de 1
x = x + i
element = Pointer sur l'élément (x + i)
Fin pour
X <- [x1, x2, x3, ...]
D <- [1, 2, 3, 4, ...]
Fonction Alldiff (factor1, factor2, factor3, factor4, factor5, factor6, factor7, factor8, factor9)
all = [factor1, factor2, ...]
total = [la valeur du nombre all0 + la valeur du nombre all1 + ...]
Si total = 45
compteur = pointer sur le compteur
compteur.value = compteur.value + 1
Fin si
Sinon
Redirection sur une page
Fin sinon
Fin fonction
Alldiff(X[0], X[1], X[2], X[3], X[4], X[5], X[6], X[7], X[8]);
Alldiff(X[9], X[10], X[11], X[12], X[13], X[14], X[15], X[16], X[17]);
Alldiff(X[18], X[19], X[20], X[21], X[22], X[23], X[24], X[25], X[26]);
Alldiff(X[27], X[28], X[29], X[30], X[31], X[32], X[33], X[34], X[35]);
Alldiff(X[36], X[37], X[38], X[39], X[40], X[41], X[42], X[43], X[44]);
Alldiff(X[45], X[46], X[47], X[48], X[49], X[50], X[51], X[52], X[53]);
Alldiff(X[54], X[55], X[56], X[57], X[58], X[59], X[60], X[61], X[62]);
Alldiff(X[63], X[64], X[65], X[66], X[67], X[68], X[69], X[70], X[71]);
Alldiff(X[72], X[73], X[74], X[75], X[76], X[77], X[78], X[79], X[80]);
/* Colonne */
Alldiff(X[0], X[9], X[18], X[27], X[36], X[45], X[54], X[63], X[72]);
Alldiff(X[1], X[10], X[19], X[28], X[37], X[46], X[55], X[64], X[73]);
Alldiff(X[2], X[11], X[20], X[29], X[38], X[47], X[56], X[65], X[74]);
Alldiff(X[3], X[12], X[21], X[30], X[39], X[48], X[57], X[66], X[75]);
Alldiff(X[4], X[13], X[22], X[31], X[40], X[49], X[58], X[67], X[76]);
Alldiff(X[5], X[14], X[23], X[32], X[41], X[50], X[59], X[68], X[77]);
Alldiff(X[6], X[15], X[24], X[33], X[42], X[51], X[60], X[69], X[78]);
Alldiff(X[7], X[16], X[25], X[34], X[43], X[52], X[61], X[70], X[79]);
Alldiff(X[8], X[17], X[26], X[35], X[44], X[53], X[62], X[71], X[80]);
/* Grand carré */
Alldiff(X[0], X[1], X[2], X[9], X[10], X[11], X[18], X[19], X[20]);
Alldiff(X[3], X[4], X[5], X[12], X[13], X[14], X[21], X[22], X[23]);
Alldiff(X[6], X[7], X[8], X[15], X[16], X[17], X[24], X[25], X[26]);
Alldiff(X[27], X[28], X[29], X[36], X[37], X[38], X[45], X[46], X[47]);
Alldiff(X[30], X[31], X[32], X[39], X[40], X[41], X[48], X[49], X[50]);
Alldiff(X[33], X[34], X[35], X[42], X[43], X[44], X[51], X[52], X[53]);
Alldiff(X[54], X[55], X[56], X[63], X[64], X[65], X[72], X[73], X[74]);
Alldiff(X[57], X[58], X[59], X[66], X[67], X[68], X[75], X[76], X[77]);
Alldiff(X[60], X[61], X[62], X[69], X[70], X[71], X[78], X[79], X[80]);
Fin fonctionCode du Sudoku
Le code que j’ai crée à été écris pour vérifier les Sudoku dans un site web. Donc j’ai utilisé de l’HTML, du CSS ainsi que du Javascript. Pour nous la partie qui nous intéresse c’est le Javascript car c’est dans ce programme que se cache l’intelligence artificielle. Pour avoir ce code vous avez juste à télécharger le programme qui est disponible ci-dessous. Bonne chance !
/* constraint satisfaction problem */
function main() {
/* Appel des éléments */
for (var i = 11; i < 92; i++) {
var x = 'x' + i;
var element = document.getElementById('x' + i);
}
const X = [x11, x12, x13, x14, x15, x16, x17, x18, x19,
x20, x21, x22, x23, x25, x26, x27, x28, x29,
x30, x31, x32, x33, x34, x35, x36, x37, x38,
x39, x40, x41, x42, x43, x44, x45, x46, x47,
x48, x49, x50, x51, x52, x53, x54, x55, x56,
x57, x58, x59, x60, x61, x62, x63, x64, x65,
x66, x67, x68, x69, x70, x71, x72, x73, x74,
x75, x76, x77, x78, x79, x80, x81, x82, x83,
x84, x85, x86, x87, x88, x89, x90, x91, x92];
/* Ensemble de variable du problèmes // Toute les entrées du sudoku mis dans un tableau X */
const D = [1, 2, 3, 4, 5, 6, 7, 8, 9];
/* Ensemble des domaines variables // Toute les possibilitées de chaque donc de 1 à 9 définit dans un tableau D[] */
function Alldiff(factor1, factor2, factor3, factor4, factor5, factor6, factor7, factor8, factor9) {
let all = [factor1, factor2, factor3, factor4, factor5, factor6, factor7, factor8, factor9];
/*console.log('Bienvenue !');
console.log(all[0].value);*/
var total = Number.parseFloat(all[0].value) + Number.parseFloat(all[1].value) + Number.parseFloat(all[2].value) +
Number.parseFloat(all[3].value) + Number.parseFloat(all[4].value) + Number.parseFloat(all[5].value) +
Number.parseFloat(all[6].value) + Number.parseFloat(all[7].value) + Number.parseFloat(all[8].value);
if (total == 45) {
// continuer
let compteur = document.getElementById('compteur');
compteur.value = compteur.value + '1';
}
else {
window.location = "file:///X:/Sudoku/sudoku_faux.html"
}
}/*
Une fonction alldiff:
variable alldiff prend la valeur vrai si la fonction alldiff est vérifié alors quitter la fonction
variable alldiff prend la valeur faux si la fonction alldiff n'est pas vérifié alors il recommence à éxecuter la fonction
alldiff() tant que la variable alldiff n'est pas egal à vrai...
CSP (constraint satisfaction problem) en Intelligence Artifielle ou Artificiel Intelligence en anglais (AI);
Ensemble des différences entre les entrées
si une valeur de du domaine D[] est égale à un ou des autre(s) valeur du domaine D[] alors un autre
domaine de variable est attribué à cette dernière tant que alldiff est faux alors recommencer
si alldiff est vrai alors finir la boucle et quitter la fonction enchainer sur une autre ligne, colonne ou case.
*/
Alldiff(X[0], X[1], X[2], X[3], X[4], X[5], X[6], X[7], X[8]);
Alldiff(X[9], X[10], X[11], X[12], X[13], X[14], X[15], X[16], X[17]);
Alldiff(X[18], X[19], X[20], X[21], X[22], X[23], X[24], X[25], X[26]);
Alldiff(X[27], X[28], X[29], X[30], X[31], X[32], X[33], X[34], X[35]);
Alldiff(X[36], X[37], X[38], X[39], X[40], X[41], X[42], X[43], X[44]);
Alldiff(X[45], X[46], X[47], X[48], X[49], X[50], X[51], X[52], X[53]);
Alldiff(X[54], X[55], X[56], X[57], X[58], X[59], X[60], X[61], X[62]);
Alldiff(X[63], X[64], X[65], X[66], X[67], X[68], X[69], X[70], X[71]);
Alldiff(X[72], X[73], X[74], X[75], X[76], X[77], X[78], X[79], X[80]);
/* Colonne */
Alldiff(X[0], X[9], X[18], X[27], X[36], X[45], X[54], X[63], X[72]);
Alldiff(X[1], X[10], X[19], X[28], X[37], X[46], X[55], X[64], X[73]);
Alldiff(X[2], X[11], X[20], X[29], X[38], X[47], X[56], X[65], X[74]);
Alldiff(X[3], X[12], X[21], X[30], X[39], X[48], X[57], X[66], X[75]);
Alldiff(X[4], X[13], X[22], X[31], X[40], X[49], X[58], X[67], X[76]);
Alldiff(X[5], X[14], X[23], X[32], X[41], X[50], X[59], X[68], X[77]);
Alldiff(X[6], X[15], X[24], X[33], X[42], X[51], X[60], X[69], X[78]);
Alldiff(X[7], X[16], X[25], X[34], X[43], X[52], X[61], X[70], X[79]);
Alldiff(X[8], X[17], X[26], X[35], X[44], X[53], X[62], X[71], X[80]);
/* Grand carré */
Alldiff(X[0], X[1], X[2], X[9], X[10], X[11], X[18], X[19], X[20]);
Alldiff(X[3], X[4], X[5], X[12], X[13], X[14], X[21], X[22], X[23]);
Alldiff(X[6], X[7], X[8], X[15], X[16], X[17], X[24], X[25], X[26]);
Alldiff(X[27], X[28], X[29], X[36], X[37], X[38], X[45], X[46], X[47]);
Alldiff(X[30], X[31], X[32], X[39], X[40], X[41], X[48], X[49], X[50]);
Alldiff(X[33], X[34], X[35], X[42], X[43], X[44], X[51], X[52], X[53]);
Alldiff(X[54], X[55], X[56], X[63], X[64], X[65], X[72], X[73], X[74]);
Alldiff(X[57], X[58], X[59], X[66], X[67], X[68], X[75], X[76], X[77]);
Alldiff(X[60], X[61], X[62], X[69], X[70], X[71], X[78], X[79], X[80]);var compteur = document.getElementById('compteur');
if (compteur.value == '111111111111111111111111111') {
window.location = "file:///X:/Sudoku/sudoku_r%C3%A9solue.html";
} else {
// ne rien faire sudoku faux.
}
};
/* Ensemble de la fonction main */
// Execution de la fonction main() dans html quand la pression du boutton "CORRECTION" est true.Le théorème des quatre couleurs
L’Australie est une fédération composée de sept états :
- Australie-méridionale
- Australie-occidentale
- Territoire du Nord
- Nouvelle Galle du Sud
- Queensland
- Tasmanie
- Victoria
Le but du théorème des quatre couleurs est d’avoir une couleur différentes pour chaque état voisin. Par exemple si l’état du Queensland est de couleur jaune comme montrer sur la carte si dessus alors les états voisins comme le territoire du Nord, l’Australie méridionale ou la nouvelle-Galles du Sud doit avoir une couleur différent que la couleur jaune. Par exemple la couleur rouge pour le territoire du Nord, la couleur verte pour l’Australie méridionale et la couleur orange pour la Nouvelles-Galles du Sud.
On peut maintenant se demander à quoi sert d’attribuer des couleurs différentes à chaque état de l’Australie. Tout simplement pour la mémoire, la mémoire retient plus vite des états avec des couleurs différentes que des états avec des même couleurs.
Les CSP avec le théorème des quatre couleurs
Comme pour le Sudoku nous allons définir le triple <X, D, C> en attribuant des valeurs différentes que les valeurs attribué au Sodoku.
Les triplet est défini comme suit :
– X est l’ensemble des états de l’Australie
– D est l’ensemble des couleurs que peu prendre une variable
– C est l’ensemble des contraintes attribué à chaque état de l’Australie
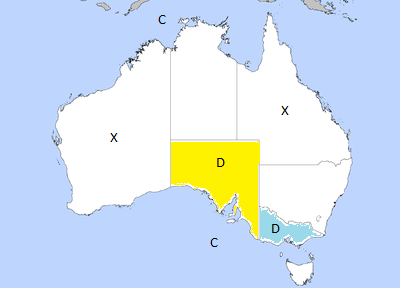
Application pratique du théorème des quatre couleurs
Nous allons définir dans la pratique l’application des états de l’Australie.
– X vaut par exemple [X0, X1, X2, X3, X4, X5, X6]
– D vaut par exemple [jaune, rouge, orange, vert, marron, blanc]
– C vaut par exemple [X0, X1, X2]
[X3, X4, X1]
[X5, X6, X2]
[X2, X4, X5, X3, X1, X0]
Pour vous aider une carte des états de l’Australie avec l’application du triplet est disponible ci-dessous.

Je crois que nous avons fait le tour pour l’application des CSP sur les états de l’Australie. Dans cet article nous avons vu que deux exemples des applications des CSPs. Evidemment pour des raisons simple nous allons pas décrire chaque problèmes que peut résoudre les CSP mais j’aimerai que nous nous évaluons globalement les possibilités.
Les possibilités des CSPs
Parmi les problèmes pouvant être modélisés par un CSP, on compte :
– Le problème des 8 dames.
– Le problème sudoku que nous avons étudié dans cet article.
– Le problème du théorème des quatre couleurs que nous avons étudié avec les états de l’Australie.
– Le problème de satisfiabilité booléenne ou problème SAT.
Dans cette section nous allons très brièvement expliquer le problème des huit dames et le problème SAT.
Le problème des huit dames
L’objectif du problème des huit dames est de placer huit dames d’un jeu d’échecs sur un échiquier classique sans que les dames ne puissent se menacer mutuellement conformément au règle du jeu d’échec.
Ce problème peut sembler simple mais est en faite un problème non-trivial (non évident ) qui sert souvent d’exemple en intelligence artificielle.
Le problème des huit dames offre 12 solutions en tenant compte de transformation telles que des rotations ou des réflexions.
En faite ce problème fait l’objet de nombreuses recherche car il peut être résolu grâce à la programmation par contrainte, la programmation logique ou avec les algorithmes génétiques même si les CSPs sont bien plus efficace pour ce problème.
Problème SAT
Enfin le problème SAT est une branche de l’informatique théorique qui exprime une formule logique propositionnelle. Il détermine s’il y existe une assignation des variables propositionnelles qui rende la formule vraie.
Les applications du problème SAT sont divers et variés :
– Le diagnostique
– La cryptographie
– La logique modale
Nous n’irons pas plus loin pour les problèmes SAT.
Merci d’avoir lu cet article. J’espère que ce dernier vous aidera dans certain projet et je vous souhaite une bonne journée.
Crédit de l’image de couverture : Tim Stellmach – CC0 1.0


![Spark 3 : à la découverte des RDD [Part 2]](https://penseeartificielle.fr/wp-content/uploads/2022/02/fire-1905608_1280-218x150.jpg)
![Installation de Spark 3 sous Windows [Part 1]](https://penseeartificielle.fr/wp-content/uploads/2022/02/pexels-fabiano-rodrigues-1662298-218x150.jpg)
