Tout pour bien démarrer dans l’intelligence artificielle (Partie 4) – Machine Learning

Maintenant que vous avez toutes les ressources pour vous auto-former, nous allons pouvoir réaliser ensemble un panel complet des différents algorithmes de Machine Learning avec des exemples pour bien en comprendre les caractéristiques principales.

Que vous cherchiez l’algorithme parfait pour votre projet ou que vous soyez « simplement » curieux, à la fin de cette lecture vous aurez enfin une carte mentale de l’IA, celle dont tout le monde parle : le Machine Learning ! Bonne lecture !

Remarque : la série est divisée en plusieurs articles :

Tutoriel 1 = sur l’IA en général et les choix techniques (langage, framework…)

Tutoriel 2 = sur les notions transverses (la donnée, les lois, la data science, hadoop…)

Tutoriel 3 = sur comment se former à l’IA, comment valoriser son savoir et surtout comment se démarquer en restant pro-actif !

Tutoriel 4 (ici) = sur le machine learning, avec tous ses algorithmes principaux en exemple : k-means, random forest, SVM…

Tutoriel 5 = sur le deep learning en détail (avec son utilisation) : réseaux de neurones artificiels, convolutifs, récurrents, etc…

Tutoriel 6 (à venir) = des grandes questions que l’on se pose sur l’IA, avec des pistes de réflexion et mon avis personnel ouvert au débat 🙂

IV. Comment bien débuter en Machine Learning

Le machine learning (ML) repose essentiellement sur les statistiques (à l’inverse du deep learning DL qui repose sur des notions de neuroscience) pour résoudre les problèmes qu’il aborde. Il est plus « simple » que le DL, mais gardez à l’esprit qu’il reste plus performant sur certains sujets ! La question n’est donc jamais de prendre l’algorithme le plus « puissant » mais bien celui qui est le plus adapté…

Deux approches : supervisée et non-supervisée

Les algorithmes supervisés sont capable d’extraire de la connaissance (i.e. de réaliser des prédictions à l’aide de données nouvelles) à partir d’un jeu de données contenant des entrées et des sorties (que l’algorithme va essayer de représenter). C’est donc typiquement une IA à laquelle on a besoin de montrer des exemples avant qu’elle puisse généraliser le concept et réaliser ses prédictions, qui peuvent être des classes (on parle de données qualitatives, nominales ou ordinales), comme MALADE vs SAIN ou des valeurs (on parle de données quantitatives, continues ou discrètes) tel le prix d’un appartement.

A l’inverse, les algorithmes non-supervisés sont ceux qui n’ont pas cette notion d’entrée/sortie, il n’y a que des données. Les algorithmes cherchent alors à réaliser des groupements pour que chaque groupe n’ait que des données « similaires entre elles » (la définition de similarité dépendant de l’algorithme). On parle souvent de clustering, le terme « cluster » signifiant grappe/groupe (puisque l’on groupe les données). A noter qu’il existe des algorithmes qui ne réalisent pas de clustering, tel celui des k-plus proches voisins et qui restent non-supervisés.

Deux types d’algorithmes supervisés : la régression et la classification

Dans les algorithmes supervisés, on distingue ensuite les problèmes de régression de ceux de classification. Il s’agit simplement de considérer le type de sortie attendue :

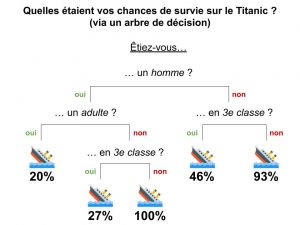
• Si la sortie (la prédiction) de l’algorithme est l’appartenance à une classe, par exemple, cette personne est SAINE, ou cette personne a survécu au Titanic, ou ce colis est encombrant, alors on parle de classification
• Si, en revanche, la sortie est un nombre, par exemple le prix d’un appartement, la taille attendue d’une personne, la probabilité d’avoir survécu au Titanic… alors on parle de régression

Attention, car tous les algorithmes ne fonctionnent pas avec ces deux types de valeurs de sortie ! Naives Bayes, algorithme qui repose sur les probabilités, ne peut être utilisé que pour de la classification, tandis qu’un arbre de décision sert pour de la classification et pour de la régression.

Quels sont les principaux algorithmes de machine learning ?

A noter qu’ils sont tous supervisés sauf K-means, kNN et l’analyse en composantes principales.

Si vous souhaitez les approfondir, n’hésitez pas à consulter l’ouvrage Data Science : fondamentaux et études de cas qui nous a bien aidé pour la rédaction de cette partie.

• la régression : linéaire univariée, linéaire multivariée, polynomiale, régularisée (ridge / LASSO / ElasticNet), logistique
• le théorème de Naive-Bayes
• le clustering : K-means, kNN
• les arbres de décision : binaire, non-binaire
• l’algorithme de Random Forest (tree bagging / feature sampling)
• le Gradient Boosting (XGBoost)
• l’algorithme de Support Vector Machine
• l’Analyse en composantes principales

Concentrons-nous sur les algorithmes en gras, qui sont très largement utilisés dans les entreprises. Il faut savoir que ces algorithmes se répartissent en deux catégories : ceux dits supervisés, qui ont des entrées et leurs sorties associées (on sait donc ce que l’on veut), et ceux dits non-supervisés, qui vont devoir construire eux-même leurs sorties pour être cohérents.

Par exemple, K-means est un algorithme non-supervisé dont le rôle est de regrouper les données en ensembles qui ont plus ou moins les mêmes caractéristiques. On ne peut donc pas lui dire comment faire (puisque notre objectif est d’avoir ce découpage) : l’algorithme doit se « débrouiller » tout seul.

a. Régression logistique (Logistic Regression) – Supervisé – Classification

Pour dire si un email relève du spam, ou si une transaction est frauduleuse voire même si une tumeur est bénigne, la régression logistique peut être utilisée car son rôle est de construire une frontière entre deux familles de données (cas binaire, sachant qu’on peut l’utiliser même si on a davantage de familles) : celles dont la prédiction peut être ramenée à 0 et celles à 1.

La régression logistique est l’équation d’une courbe qui vient séparer les données en deux parties distinctes. Bien évidemment, cette courbe ne peut pas « prendre tous les tournants » qu’on souhaite, elle reste assez simple :

\(\sigma(t) = \frac{1}{1 + \exp^{-t}}\) avec par exemple t qui est affine en x (l’entrée de l’algorithme) : \(t = \beta_1 \cdot x + \beta_2\)

b. K-means clustering (K-moyennes en français) – Non-supervisé

Passons maintenant à un algorithme bien différent mais tout aussi utile : celui des K-moyennes. On se donne un nuage de points, représentant par exemple les produits vendus par votre magasin, avec leurs caractéristiques. Vous voulez alors qu’ils soient divisés en 4 catégories de produits qui se ressemblent. Comment faire ?

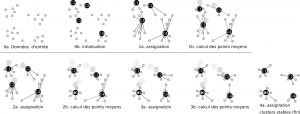
K-means va commencer par placer 4 points au hasard : ce seront les centres de votre cluster. Ensuite, il va, pour chaque produit de votre boutique, calculer la distance qui le sépare des 4 centres et le rattacher au plus proche. Une fois que tous les points auront été attribués, pour chaque groupe, on va calculer la valeur moyenne : cette valeur devient la nouvelle position du centre, et on réaffecte tous les produits en calculant leur distance !

Après un certain nombre d’étapes, les centres arrêtent de se déplacer (en général). A noter que leur position dépend souvent du nombre K que l’on a choisi, et de l’initialisation. Il faut donc lancer l’algorithme plusieurs fois et ne retenir que la meilleure configuration par rapport à ce que l’on attend du processus…

c. k-Nearest Neighbors (kNN) – Supervisé – Classification

A ne pas confondre avec K-means, car les deux algorithmes se ressemblent dans l’idée.

Ici, on souhaite, pour un nouveau produit, prédire à quelle famille il appartient grâce à ses caractéristiques. Dans nos données d’apprentissage, on a tous les produits de notre entreprise déjà rangés en familles (par exemple, produits encombrants et produits non-encombrants, en ayant les dimensions des produits).

Pour déterminer la classe (la famille) d’un nouveau produit, k-Nearest Neighbors, qui signifie les K voisins les plus proches, va regarder quels sont les k produits les plus proches en termes de distance (cela ressemble donc à k-means), puis regarder la classe de ces k produits, avant de répondre par la classe la plus représentée. Si k=10, qu’on a 7 produits encombrants proches et 3 qui ne le sont pas, alors on dira que le produit est encombrant.

A noter qu’une fois encore, les performances vont dépendre de la valeur k choisie (généralement entre 3 et 15).

d. Arbres de décision (Decision Tree) – Supervisé – Régression ou Classification

Un arbre de décision est une succession de questions dont les réponses vont nous amener à des conclusions différentes. Par exemple :

• Question 1 (on parle de racine): est-ce que l’animal a des ailes ?
  • Question 1.1 s’il a des ailes (on parle de noeud) : est-ce qu’il représente les Etats-Unis ?
    • Réponse 1 si oui (on parle de feuille de l’arbre) : c’est un Pygargue à tête blanche
    • Question 1.1.2 si non…
  • Question 1.2 s’il n’a pas d’ailes : est-ce un mammifère ?
    • …

Très faciles à interpréter (on comprend directement la prédiction de l’algorithme en regardant les choix successifs), ils reposent très souvent sur des probabilités pour être construits. Pour l’exemple de nos animaux ci-dessus, l’IA aura analysé les caractéristiques de plein d’animaux avec la prédiction associée (nom de l’animal) avant de remarquer que si elle demande en premier « y a-t-il des ailes » alors il y a autant de réponses positives que négatives. Cette question représente donc un bon critère. Ensuite, dans chaque sous-groupe, l’IA cherche la question qui va de nouveau diviser en deux groupes de même taille les réponses, et ainsi de suite jusqu’à atteindre la profondeur maximale souhaitée.

e. Random Forest (RF) – Supervisé – Régression ou Classification

De quoi est composé une forêt aléatoire ? D’arbres décisionnels tout simplement !

Random Forest (ou forêt aléatoire ou forêt d’arbres décisionnels) est ainsi plusieurs arbres de décisions (2, 3, 10, …) que l’on consulte tous en parallèle pour avoir leur « avis », avant de décider de la prédiction finale. Il y a quand même plusieurs subtilités à apporter :

• les arbres de décision n’ont pas été entraînés sur les mêmes données ! On part d’un jeu de données global, et pour entraîner chaque arbre, on ne sélectionne qu’une partie aléatoire des données. De cette manière, chaque arbre sera différent et aura une vision différente du jeu de données. On peut également supprimer des colonnes entières (par exemple l’âge des passagers du Titanic)
• Si l’objectif est de prédire une classe (« survivant » ou « décédé », un problème de classification), alors on procédera à un vote des arbres (2 sont pour « survivant » et 1 est pour « décédé », donc la personne est considérée survivante). Si on cherche à prédire une valeur (probabilité de survie, un problème de régression), alors on réalisera la moyenne des valeurs prédites (80% et 90% pour les deux premiers arbres, 40% pour le troisième, alors la prédiction finale sera de 70%)
• Enfin, plusieurs astuces existent pour améliorer ses prédictions globales. Par exemple, on peut attribuer une note de confiance à chaque arbre en fonction de la qualité de ses prédictions, et tenir compte de cette note pour la prédiction suivante (un arbre qui a souvent juste aura plus de poids dans le vote final).

f. Support Vector Machine (SVM) – Supervisé – Régression ou Classification

Attaquons-nous à un monument de la data science : la Machine à Vecteurs de Support (ou Séparateur à Vaste Marge…).

Le principe général du SVM est assez proche de la régression linéaire : on a un ensemble de données, par exemple nos objets encombrants, et le but est de construire une droite (on parle « d’hyperplan » car il n’y a pas que deux axes de données mais beaucoup plus : « hauteur du colis », « longueur », « largeur », « poids »…) qui va séparer les objets encombrants de ceux normaux, dans l’optique d’appliquer une taxe supplémentaire.

Si on ne garde que l’information « volume du colis » en fonction de « poids du colis », alors on peut imaginer plusieurs manières de tracer la droite entre les deux ensembles de points, où les carrés bleus représentent les objets normaux et les ronds rouges les objets encombrants.

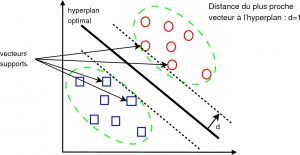
En régression linéaire, n’importe quelle droite ferait l’affaire, mais pour SVM, le but va être de choisir la droite la plus « équilibrée » par rapport à notre jeu de données. Concrètement, cela signifie que SVM va garder la droite qui est la plus éloignée de tous les points ! Pour faire ça, il suffit de calculer la distance de la droite à chaque point (on rappelle qu’il s’agit de la longueur à « angle droit » qui les sépare) et de ne garder que la plus petite valeur. Ensuite, la droite sélectionnée sera celle pour laquelle cette plus petite valeur est la plus grande…

• SVM permet donc de séparer les deux groupes en gardant le plus de marge possible (donc de capacité à généraliser)
• Lorsque l’on a plus de 2 classes, SVM (on parle de SVM multiclasse) fonctionne très bien en procédant ainsi : construire la première droite qui sépare « classe 1 » de toutes les autres classes puis construire la deuxième droite qui sépare « classe 2 » de toutes les autres classes, et ainsi de suite, puis on regroupe toutes ces droites

• 

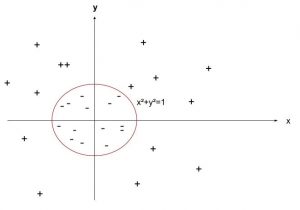
  Souvent, les données ne sont pas séparables, c’est-à-dire qu’il y a toujours des exceptions (dites slack variables) qui se retrouvent au milieu d’une autre classe : impossible alors de construire une droite parfaite. La technique est de construire la droite qui sépare au mieux avec une erreur (données mal classées) la plus faible possible. On a donc un équilibre à gérer entre erreur commise et distance de séparation

• Enfin, il existe des astuces mathématiques pour accélérer les calculs de SVM qui peuvent vite se complexifier (kernel trick), ainsi que des astuces pour traiter des données non-linéairement liées : on utilise des « noyaux » qui vont transposer le problème de manière à ce qu’il soit traitable (mais ce n’est pas toujours possible !).

g. Principal Component Analysis (PCA) – Non-supervisé

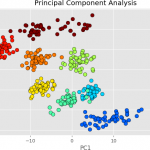
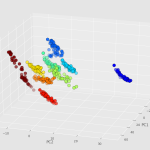
Imaginons que l’on ait un ensemble de données, par exemple des colis avec le poids, les dimensions (longueur, largeur, hauteur), l’information de s’il est considéré encombrant ou non. On cherche alors à voir un peu comment se répartissent les données dans l’espace… Sauf qu’il y a 5 variables, donc il faudrait représenter un espace avec 5 dimensions… Ce qui est impossible à interpréter.

Le rôle de PCA est de réduire cette dimension à 2 ou 3 (pour ce cas-ci), en essayant au maximum d’avoir une représentation fidèle aux données d’origine. Ce travail est difficile, mais présente un grand intérêt puisqu’il nous donne accès à une visualisation du jeu de données !

On peut donc considérer que l’on a créé deux nouvelles colonnes pour nos données (ce sont les deux axes du changement de dimension), et qu’on les a alimentées de manière à ce qu’une représentation des données suivant ces deux paramètres soit « équivalente » à une représentation des données avec tous les paramètres !

Concrètement, voici un exemple métier pris sur le site idtools qui vous aidera à y voir plus clair (et qu’on vous conseille de lire si PCA vous intéresse !) :

• Grâce à un spectroscope, on scanne un échantillon de lait
• L’objectif va être, pour un nouvel échantillon, de dire quel est son « taux de lactose » (0, 1/8e, 2/8e, 3/8e, 4/8e, 5/8e, 6/8e, 7/8e ou 8/8e) en le comparant avec les autres échantillons de lait (et dont on a déjà déterminé ce taux), bien évidemment sans pouvoir le « mesurer » directement !
• Pour chaque échantillon, le spectroscope prend… 600 mesures différentes. On a donc un espace à 600 dimensions !
• C’est là qu’intervient PCA : grâce à lui, on va pouvoir trouver deux axes notés P1 et P2 qui n’existent pas encore (par exemple, une combinaison « bizarre » des mesures n°3, 345 et 602) mais qui, lorsqu’on projettera les données dans ce nouvel espace, permettront d’avoir un graphique « lisible » et bien ordonné.

Explication plus « technique » : PCA repose sur des matrices et plus particulièrement sur des vecteurs propres. Grâce à la matrice de variance covariance (ou de corrélations), on analyse la dispersion des données considérées (moyenne, variance, écart-type…) i.e. les liaisons entre les variables et les ressemblances entre les données. L’espace est alors déformé de manière à ce que le nouveau « premier axe » créé disperse au maximum l’inertie des données (i.e. on veut que la somme des carrés de toutes les distances des points au centre de gravité des données soit maximale), pour avoir un maximum de lisibilité et de variabilité. Ensuite, le second axe vient aider à séparer davantage les données qui ne l’ont pas été suffisamment par le premier axe, et ainsi de suite.

NB : PCA est également appelée Karhunen-Loève Transform (ou Theorem) s’il concerne le milieu du traitement du signal ou de l’analyse d’images. Les termes sont bien équivalents.

Conclusion sur le Machine Learning

Au final il existe de nombreux algorithmes de machine learning, chacun avec ses avantages, ses inconvénients, et ses cas d’application. Par exemple, on a vu la différence entre algorithme supervisé et non-supervisé, qui est déterminante, ainsi que la notion de classification et de régression, termes omniprésents dans l’univers du machine learning.

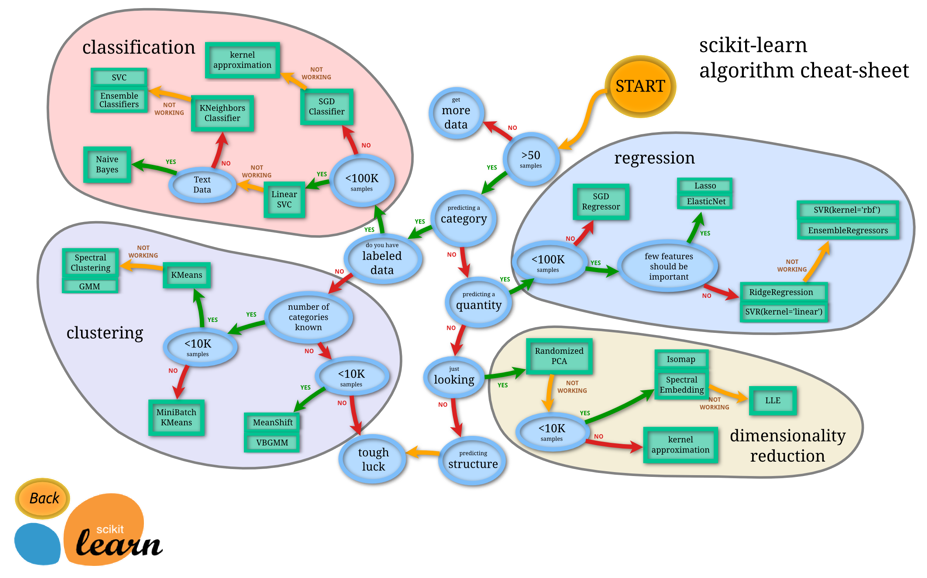
Enfin, bien souvent, pour un problème donné, on se retrouve à tester plusieurs algorithmes en faisant varier les paramètres, mais si cela peut vous aider… Voici un arbre de décision pour choisir le bon algorithme adapté à vos besoins !

On espère que cette partie vous aura bien aidé à débuter en Machine Learning (n’hésitez pas à nous dire en commentaire).

Crédit de l’image de couverture : geralt – Pixabay License