L’une des capacités fondamentales de l’humain est celle d’analyser son environnement. Dans la majorité des cas, cela passe par la reconnaissance des éléments de notre champ de vision : trouver les autres personnes, identifier les voitures, les animaux…
Jusqu’à l’émergence des réseaux de neurones convolutifs, en 2012 avec Alex Krizhevsky, la tâche était difficile pour un ordinateur. Heureusement, l’approche de ces réseaux inspirés de notre oeil (plus particulièrement du fait que certains neurones de notre aire visuelle ne réagissent qu’aux bordures verticales et d’autres aux horizontales/diagonales) a ouvert de nombreuses applications, que ce soit en imagerie médicale, véhicules autonomes, reconnaissance faciale, et même analyse de textes.
Dans ce focus, nous allons voir ce qu’est un réseau neuronal convolutif puis nous en implémenterons un ensemble !
PS : « convolutionnel » est une erreur de traduction couramment faite. Ceci étant, le mot est utilisé parfois dans l’article pour… des raisons de référencement (désolé !). Pensez à bien utiliser le mot « convolutif » de votre côté !
I. Partie théorique pour bien comprendre le réseau convolutif
Nous allons voir ensemble comment fonctionne le réseau convolutif, en abordant brièvement le principal outil mathématiques caché derrière, ainsi que toutes les étapes de l’analyse faite par l’algorithme.
Principe général
Si nous, en tant qu’humains, voyons les images avec des formes et des couleurs, l’ordinateur, lui, ne voit que des nombres organisés comme suit :
- 16×16 pixels pour l’image du robot (ci-après), où le premier 16 est la largeur de l’image et le second est la hauteur
- 3 couches de ces 16×16 pixels, chacune correspondante à une coloration : rouge (r pour red), vert (g pour green), bleu (b pour blue), ou 4 couches pour des images « PNG », avec la 4ème couche étant l’alpha (a) = la transparence du pixel
Ce qui nous donne ici une matrice 3D de taille 16x16x3.
Remarque : le blanc est composé à 100% de rouge, vert et bleu (d’où le 255 tout autour du robot). De plus, si on regarde par exemple les positions (3,4) et (7,7), on voit bien que le rouge est très présent (valeur proche de 255 dans le channel rouge) alors que les autres couleurs sont absentes (valeur proche de 0).
Le réseau de neurones convolutionnel va ainsi recevoir cette image (vue comme une matrice), et appliquer un certain nombre d’opérations de deux catégories :
- les filtres, pour faire ressortir, par exemple, les arêtes verticales, les variations de coloration, etc…, sachant que plus les filtres interviennent tard dans l’enchaînement, plus ils permettent de détecter des formes complexes (et plus abstraites)
- les simplifications, pour alléger les calculs et dégager les informations principales
Ensuite, il donnera la probabilité que cette image représente un robot, un chien, un humain… grâce à un « réseau de neurones artificiels » (autre type de réseau, que l’on a déjà étudié dans le focus sur le perceptron).
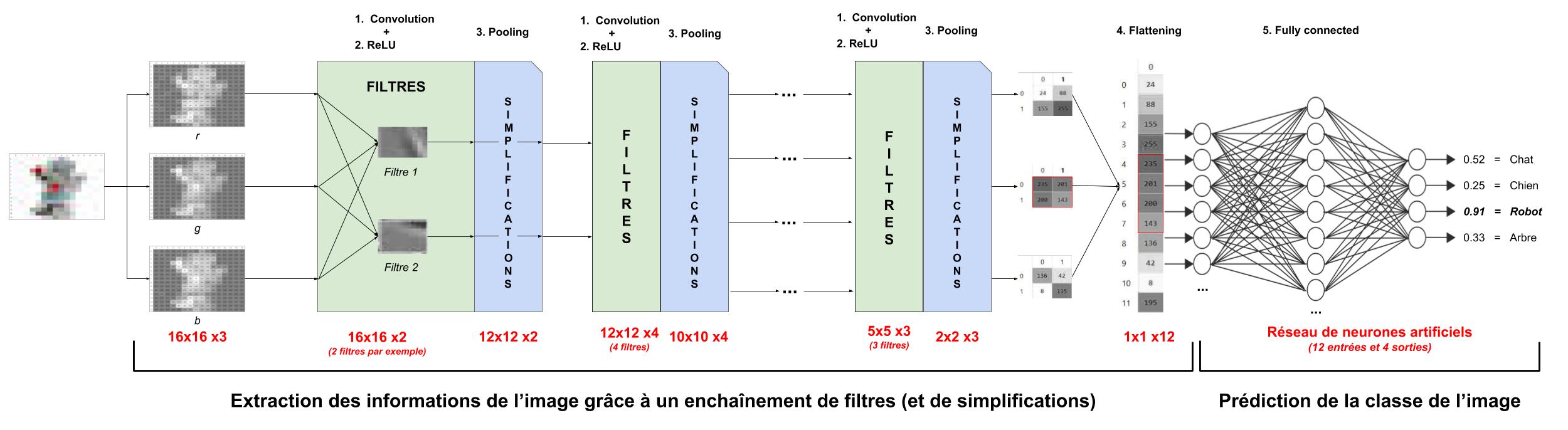
1. L’opération de convolution
La convolution est le cœur du réseau de neurones convolutif, comme vous vous en doutez.
A l’origine, une convolution est un outil mathématique (on parle de produit de convolution) très utilisé en retouche d’image car il permet d’en faire ressortir des caractéristiques :
- Mise en évidence des traits verticaux, horizontaux, diagonaux…
- Floue de l’image (blur), lissage des textures ou à l’inverse « sharpen »
- Inversion de couleurs
- etc…
… sous réserve d’appliquer le bon « filtre« . En fait, une convolution prend simplement en entrée une image et un filtre (qui est une autre image), effectue un calcul, puis renvoie une nouvelle image (généralement plus petite).
Les filtres
On a vu des exemples de filtres connus ci-dessus. Cependant, dans la pratique, les filtres d’un réseau de neurones convolutif ont un kernel, stride, padding défini à l’avance MAIS leurs valeurs sont générées aléatoirement à l’initialisation. Ensuite, lorsque le réseau apprend, les valeurs des filtres sont mises à jour pour améliorer les résultats du CNN : les valeurs des filtres font donc parties des variables (poids, biais…) que le réseau change en apprenant !
Le « transfer learning » consiste à utiliser un CNN déjà entraîné pour une tâche particulière afin de le spécialiser à un autre problème. Par exemple, on peut réutiliser une IA de reconnaissance d’avions pour identifier des hélicoptères assez facilement car les filtres optimisés pour différentier les avions ont de grandes chances de fonctionner aussi sur des hélicoptères ! On évite ainsi la longue phase d’entraînement où les filtres sont modifiés pour trouver ce qui est pertinent (discriminant) dans une image…
Enfin, il est bon de noter que les filtres se complexifient au plus la convolution intervient tard dans le CNN, au sens où ils détectent des formes de plus en plus complexes. En effet, après plusieurs applications de filtres, les images ne ressemblent plus beaucoup à l’image d’origine (il n’en reste que les informations « principales » décidées par les filtres précédents). Là où une première convolution fera ressortir les traits verticaux, la dernière convolution sera capable de trouver des structures en nid d’abeille (grâce aux transformations de l’image) : le CNN aura accumulé les détails pour en trouver l’idée globale.
Calcul de la convolution
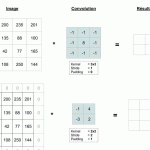
Le calcul est relativement simple : pour une convolution de taille 3×3, on va sélectionner dans l’image les 3×3 premiers pixels pour en créer un nouveau dans l’image de sortie. La valeur de ce nouveau est égale à « pixel1 de la sélection dans l’image » * « pixel1 du filtre » + « pixel2 de la sélection dans l’image » * « pixel2 du filtre » + etc… jusqu’au neuvième pixel.
Cette taille de 3×3 est appelée le kernel (noyau en français).
Ensuite, pour calculer la deuxième valeur de l’image de sortie, on va utiliser le paramètre « stride » de la convolution. Il représente de combien de pixels dans l’image d’entrée on va se décaler pour ré-appliquer la convolution (cf le gif animé ci-dessous) !
Vous aurez sans doute deviner qu’il peut arriver que la convolution dépasse de l’image si on choisit mal le kernel et le stride. Par exemple, pour une image 4×4, un kernel de 2×2 et un stride de 3, on va avoir un problème après la première convolution. De plus, vous aurez remarqué que le résultat de la convolution est une image plus petite que l’image d’entrée. A ces deux problèmes, on a un paramètre « padding » qui est utilisé dans les convolutions et qui, simplement, ajoute des 0 autour de l’image d’entrée, pour augmenter la taille de l’image de sortie ou éviter les dépassements.
Les différentes convolutions
Il existe plusieurs types de convolutions, même si en général on utilise celle de base, il peut s’avérer utile de connaître les outils à notre disposition.
- La convolution classique, dont nous avons parlé ci-dessus et qui est constamment utilisée. Elle a trois paramètres : la taille de la convolution (appelé kernel et souvent en 3×3), le stride qui représente le décalage du kernel entre chaque calculs, et le padding qui est la manière dont on peut « dépasser » de l’image pour appliquer la convolution
- La dilated convolution, identique à la convolution à ceci-près que le kernel est éclaté (on prend, par exemple, un pixel sur deux pour calculer la convolution). Il y a un paramètre supplémentaire : le dilation rate, qui est le nombre de pixels à ignorer
- La transposed convolution, qui construit la sortie comme si on inversait une convolution sur l’image
- La separable convolution, qui est une convolution décomposable en convolutions plus simples
Voici des GIF animés qui vous aideront à y voir plus clair :
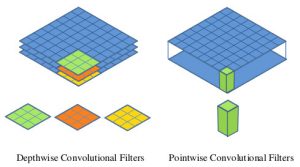
Revenons brièvement sur la separable convolution, car elle n’est employée que dans de rares cas. Une convolution classique est appliquée indépendamment sur chaque channel, ce qui donne 3 images en partant de l’image d’origine décomposée en RGB. Ces 3 images sont ensuite ajoutées entre elles (pixel à pixel) pour former le résultat final de la convolution. Le nombre de calculs est donc élevé (rappelons qu’on a souvent 64, 128, 256 ou 512 channels). Une pointwise separable convolution (cas de convolution séparable utilisée en deep learning) a pour particularité de pouvoir être calculée directement sur tous les channels en même temps. On va donc calculer la convolution d’un seul pixel sur tous ses channels, et ça nous donnera une valeur. On fera de même avec les autres pixels, un à un (toujours transversalement i.e. en profondeur), et on aboutira sur une image directe (sans avoir à en ajouter plein à la fin) ! C’est le principe du MobileNet-SSD ! La version depthwise separable convolution ressemble à la version classique, à ceci près que la décomposition de la convolution permet de gagner une partie des calculs (cf le très bon article en anglais de TowardsDataScience).
2. La couche ReLU (rectification linéaire)
La fonction d’activation ReLU est une fonction dite « rectifier » très utilisée en Deep Learning. Dans les réseau de neurones convolutionnels, elle est appliquée très souvent en sortie d’une couche de convolutions pour diverses raisons :
- Comme on l’a vu, une convolution va réaliser des opérations d’additions/multiplications : les valeurs en sorties sont donc linéaires par rapport à celles en entrée.
- Or, dans une image, la linéarité n’est pas très présente ni importante (par exemple, les variations entre valeurs de pixels peuvent être importantes dans une région, l’image a des coins…).
- ReLU, de par sa définition, est une fonction qui vient briser (une partie de) la linéarité en supprimant une partie des valeurs (toutes celles négatives) !
- En supprimant une partie des données, ReLU permet également d’accélérer les calculs
- En ne modifiant pas les données positives, ReLU n’impacte pas les caractéristiques misent en évidence par la convolution, au contraire : elle les met davantage en évidence en creusant l’écart (valeurs négatives) « entre » deux caractéristiques (par exemple le nez et les yeux).
Que fait exactement ReLU ? Elle remplace tous les nombres négatifs par la valeur 0.
A noter qu’il existe d’autres ReLU, comme par exemple Leaky ReLU, qui cassent moins la linéarité des données, même si ReLU est très largement préférée et utilisée.
3. Le pooling
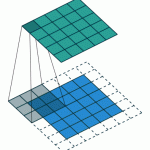
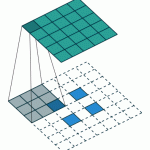
Le pooling est une opération simple qui consiste à remplacer un carré de pixels (généralement 2×2 ou 3×3) par une valeur unique. De cette manière, l’image diminue en taille et se retrouve simplifiée (lissée).
Pour appliquer le pooling, on commence par sélectionner un carré de pixels de taille 2×2 (pour un pooling de 2×2) puis on calcule la valeur qui va venir remplacer ce carré (cf type de pooling ci-après). Ensuite, on décale ce carré vers la droite de 1 cases si le stride (= pas) vaut 1 par exemple (généralement, il vaut 1 ou 2).
Plusieurs stratégies sont envisageables si la sélection sort de l’image : on peut ne rien calculer, ou calculer malgré tout en ignorant les pixels manquants. Mais en général, le stride est étudié pour que la sélection rentre parfaitement partout.
Une fois arrivé au bout à droite, on recommence tout à gauche en décalant une fois vers le bas (d’un pas égal au stride) et en allant de nouveau vers la droite.
Il existe plusieurs types de pooling :
- Le « max pooling« , qui revient à prendre la valeur maximale de la sélection. C’est le type le plus utilisé car il est rapide à calculer (immédiat), et permet de simplifier efficacement l’image
- Le « mean pooling » (ou average pooling), soit la moyenne des pixels de la sélection : on calcule la somme de toutes les valeurs et on divise par le nombre de valeurs. On obtient ainsi une valeur intermédiaire pour représenter ce lot de pixels
- Le « sum pooling« , c’est la moyenne sans avoir divisé par le nombre de valeurs (on ne calcule que leur somme)
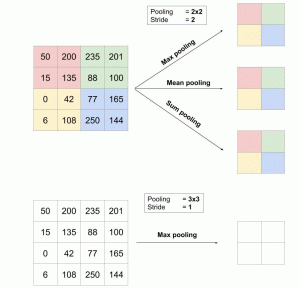
Quelle différence entre les trois ? Mean et sum sont quasi-identiques, j’ai du mal à voir un cas où la différence serait significative. On peut simplement noter que « sum » fait augmenter la valeur des pixels de l’image, tandis que mean permet de rester borné : le premier aura donc tendance à creuser les écarts entre régions de l’image, ce qui peut mettre en avant certaines caractéristiques.
En revanche, entre max et mean, la différence est plus flagrante (et importante) : de par sa nature, max-pooling va avoir tendance à retenir les caractéristiques (features) les plus marquées et simples de la sélection de pixels, comme par exemple une arête verticale. A l’inverse, mean étant une moyenne, seules les features moins marquées ressortiront.
De manière générale, il est recommandé d’utiliser max-pooling, car il se distingue de mean-pooling sur les cas extrêmes et est quasiment équivalent à mean-pooling dans les autres cas !
4. Le flattening (ou mise à plat)
Dernière étape de la partie « extraction des informations », le flattening consiste simplement à mettre bout à bout toutes les images (matrices) que nous avons pour en faire un (long) vecteur. Les pixels (en réalité ce ne sont plus des images ou des pixels, mais des matrices de nombres, donc les pixels sont ces nombres) sont récupérés ligne par ligne et ajoutés au vecteur final.
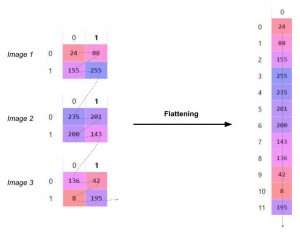
Quel est l’intérêt de cette étape ? En fait, le réseau de neurones (étape 5) prend simplement en entrée un vecteur (à chaque neurone d’entrée on envoie une seule valeur) !
Par conséquent, dans l’absolu, rien n’empêche d’utiliser un flattening qui lit les matrices par colonne, ou même qui mélange tous les « pixels » (sans en changer les valeurs), tant que le procédé de flattening reste toujours le même.
5. La partie « fully connected » ou « dense » alias le réseau de neurones artificiels
Ayant déjà écrit un article sur le sujet, nous n’allons pas nous étendre dessus ici. Je vous invite à découvrir le perceptron multi-couches, qui est utilisé comme réseau fully-connected /dense pour la prédiction de la classe de l’image.
De manière synthétique, un réseau de neurones artificiels est un réseau qui contient des neurones :
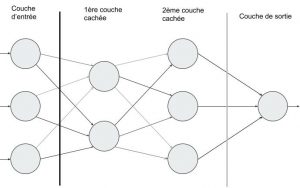
- les neurones d’entrée, qui envoient leur valeur à tous les neurones de la couche suivante. Dans le cas du CNN, ce sera la valeur d’un pixel précis pour chaque neurone (tout simplement, en suivant l’ordre du vecteur)
- les neurones cachés, organisés en couches, qui vont envoyer la somme des signaux qu’ils reçoivent (pondérés par « l’importance » de leur liaison) aux neurones de la couche suivante
- les neurones de sortie, qui reçoivent la somme des signaux pondérés de la dernière couche cachée
Chaque neurone de sortie représente alors une prédiction spécifique. Par exemple, le premier neurone représente la prédiction « c’est un chat », le deuxième « c’est un chien », etc… Et la conclusion de notre réseau dépend de quel neurone de sortie a le signal le plus fort !
=> Notre partie fully connected reçoit donc un vecteur de nombres et renvoie des probabilités pour chaque classe de prédiction. On fait alors ce qu’on veut de ces probabilités, soit prendre la plus grande, soit n’en garder aucune si elles sont trop faibles, soit…
A noter que les fully connected (ou dense) des réseaux convolutionnels n’ont que deux couches : celle d’entrée et celle de sortie. Puisque celle d’entrée dépend systématiquement du nombre de sorties de la couche précédente, on ne précise que le nombre de sorties du fully connected ! Il sera donc normal de trouver par la suite « un réseau de neurones artificiels de 10 neurones », car il est sous-entendu que ce sont 10 neurones de sortie (et pas « en tout », car il faut y ajouter les neurones d’entrée) et qu’il n’y a pas de couche cachée.
6. Mise bout à bout du réseau neuronal convolutif
Nous avons à présent tous les outils pour comprendre l’architecture d’un réseau de neurones convolutif. Il en existe plusieurs dans la littérature dont l’efficacité varie en fonction de la tâche, car ils n’ont pas tous le même nombre de convolutions (ni la même structure).
Citons notamment :
- LeNet (le plus simple, pour découvrir les CNN),
- AlexNet (lancé en 2012),
- ZFNet (amélioration d’AlexNet tombée dans l’oubli),
- GoogLeNet (parent du célèbre Inception, un algorithme de reconnaissance d’image avec d’autres subtilités, au même titre que YOLO, MobileNet, etc…),
- VGGNet (encore très utilisé et puissant),
- ResNet (pareil, même s’il s’éloigne d’un CNN traditionnel)
Je vous propose de lire la structure de VGG16 ensemble, la version « 16 couches » (on ne compte que les convolutions et les denses) de VGG :
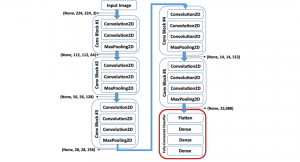
- On a dans le premier bloc de convolutions : 2 convolutions successives à 64 filtres, suivies d’une étape de pooling
- On réitère ce type d’architecture jusqu’au dernier bloc de convolutions, puis on flatten
- Enfin, on enchaîne 3 réseaux de neurones artificiels (appelés Dense)
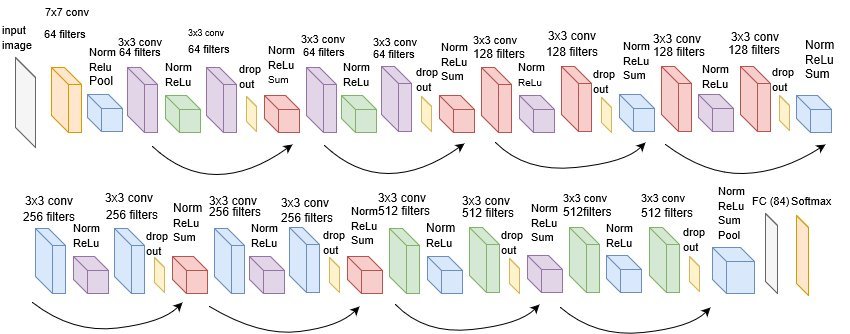
Maintenant regardons de quoi est fait le ResNet-18, la version à 18 couches du ResNet (à noter que ResNet signifie Residual Network) :
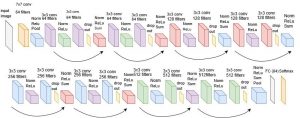
- Des convolutions suivies de normalisations, de pooling et/ou de ReLU
- Des « dropout« , phases dans lesquelles on désactive une partie aléatoire de neurones pour forcer le CNN à s’adapter à un manque d’informations
- Des « sum » où on ajoute simplement les données
- Une couche fully-connected (FC), parfois ignorée dans la pratique car on ne veut pas toujours prédire une classe précise)
- Et enfin un « softmax » qui est une étape purement mathématique qui normalise le vecteur de sortie pour qu’il représente des probabilités (ça ne change en rien l’ordre des prédictions, les valeurs de sortie sont simplement ramenées entre 0 et 1 de sorte à ce que leur somme fasse 1).
Remarque : on vous laisse le soin de trouver la formule de la dimension des images après une convolution !
Vous ne trouvez pas ? La voici :
\(O = \frac{I – K + 2 \cdot P}{S} + 1\)avec :
- O : taille de l’image de sortie (largeur)
- I : taille de l’image d’entrée (largeur)
- K : taille du kernel utilisé (largeur)
- N : nombre de filtres
- S : le stride appliqué
- P : le padding appliqué
Remarque : c’est pareil pour la hauteur de l’image.
Par exemple, pour une convolution 2×2 de stride 2 et de padding 1 appliquée à une image 4×4, on obtient une image de sortie de taille :
\(O = \frac{I – K + 2 \cdot P}{S} + 1 = \frac{4 – 2 + 2 \cdot 1}{2} + 1 = 3\)Bonus : le padding
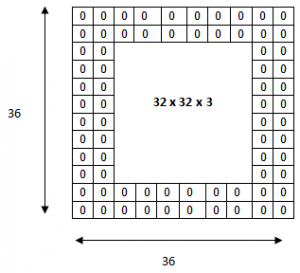
Parfois, il peut être intéressant de conserver une certaine dimension dans les tailles des images en sortie des convolutions. Le padding consiste simplement à ajouter des 0 tout autour d’une matrice (image) pour en augmenter la taille.
Par exemple, un padding de 2 sur une matrice de taille 32×32 ajoutera des 0 à gauche sur 2 colonnes, à droite sur 2 colonnes, en haut sur 2 lignes et en bas sur 2 lignes !
Bonus : comment et qu’apprend le réseau convolutif ?
Commençons par répondre à la question « quoi« . En général, lorsqu’on pense à un réseau de neurones, on a en tête les neurones reliés entre eux par des poids (les liaisons). C’est la mise à jour de ces poids qui permet de spécialiser un réseau de neurones dans une tâche précise, comme par exemple la reconnaissance faciale, la prédiction du temps météorologique ou d’une panne industrielle…
Cependant, avec le réseau de neurones convolutifs, il n’y a pas au sens littéral de neurones, à l’exception de ceux dans la couche fully-connected (qui vont donc faire partie des éléments qui évoluent dans le CNN)… mais il y a des convolutions, et, avec elles, des filtres ! Vous voyez où je veux en venir ? Voici ce qui se met à jour dans un CNN :
- Les matrices des filtres des convolutions changent (en revanche, la taille du kernel, le nombre de filtre, etc… reste fixe). Ainsi, une convolution 2×2 qui vaut par exemple [[0,1],[2,3]] à l’itération (epoch) 1, vaudra à l’itération 2 : [[-0.3,1.01],[2.4,2.85]], et continuera de changer si cela permet d’améliorer les résultats du CNN (loss) !
- Dans ces matrices, il y a un élément dont nous n’avons pas parlé car il est masqué : le biais. Lorsque l’on déclare une convolution 3×3, on ne choisit pas dans la pratique les nombres qui vont alimenter la matrice, ils sont tirés aléatoirement lors de l’initialisation puis sont mis à jour (cf point précédent). De plus, une valeur externe pour chaque matrice est définie aléatoirement à l’initialisation et ajoutée à la matrice après le calcul de la convolution ! Pour chaque filtre, on va donc calculer la convolution entre l’image et le filtre puis ajouter à chacun des pixels résultant un certain nombre (le même pour un même filtre). Ce fameux biais est ensuite modifié pour chaque filtre lors de la phase d’apprentissage de l’algorithme.
- Enfin, il y a les poids entre les neurones dans les couches fully-connected, ainsi que le biais associé à ces neurones (vous pouvez consulter le perceptron multi-couches pour plus de détails).
Répondons enfin au « comment » de manière assez courte car le détail est déjà donné dans le perceptron multi-couches également : un algorithme dit de « backward propagation », généralement le « gradient descent » (cf le TP) est appliqué.
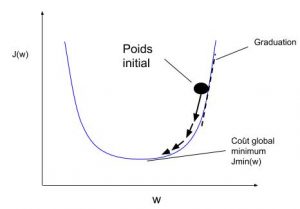
Concrètement, le gradient descent va regarder quelle est la prédiction faite (par exemple le vecteur (0.5,0.6,0.2) pour une donnée d’entrée (une image de chien). Il va comparer cette prédiction à la valeur attendue (il faut donc la connaitre, par exemple (1,0,0)) et constater que la première valeur est beaucoup trop faible, la deuxième trop élevée et la troisième un petit peu trop haute. En parcourant les paramètres modifiables (cf le paragraphe précédent), l’algorithme va les mettre à jour à tour de rôle pour essayer d’améliorer le résultat final et réduire l’écart entre la prédiction et la réalité !
Remarque : lorsque l’apprentissage se fait par batch, l’erreur commise est calculée sur l’ensemble du batch puis le CNN est mis à jour en fonction de l’erreur globale et non celle de chaque image.
Remarque : bien entendu, il y a des mathématiques derrière cet algorithme de gradient descent, et la mise à jour n’a rien d’aléatoire : on sait, pour chaque paramètre, s’il doit être augmenté ou diminuer, et l’ampleur de la mise à jour à faire pour se rapproche d’une meilleure solution !
Bonus : le fine-tuning (alias le transfer learning) ou la possibilité d’adapter un autre CNN à ses besoins !
Pour conclure cette partie sur la théorie des réseaux de neurones convolutifs, je vais vous parler brièvement du « fine tuning« .
Il s’agit d’une technique consistant à prendre un CNN entraîné pour résoudre un problème spécifique, et de l’adapter à un autre problème assez proche. Par exemple, transformer un CNN qui détecte les voitures en un CNN qui détecte les camions ! Cela permet de gagner beaucoup de temps et de parvenir à d’excellents résultats sans avoir une grande puissance de calcul.
De manière plus pragmatique, comment faire ?
Comme nous l’avons vu, les premières couches d’un CNN vont se spécialiser dans la découverte de structures simples dans l’image (lignes horizontales, verticales…) tandis que les dernières convolutions mettront en avant les formes complexes (une jante de roue ou la forme de l’habitacle d’une voiture par exemple).
De plus, le réseau de neurones dit « dense » en fin de CNN prédira une réponse directement liée à ce qu’il a appris à reconnaître à l’origine.
Pour fine-tune un CNN il suffit donc :
- De « freeze » (i.e. les paramètres internes ne peuvent plus être modifiés) les premières couches de convolutions du CNN
- De supprimer complètement la dernière couche (dense) du CNN et de la remplacer par une nouvelle couche répondant à notre nouveau cas d’utilisation (bon nombre de neurones en sortie)
- De diminuer la vitesse d’apprentissage : en effet, les couches de convolutions sont déjà plutôt bien entraînées pour reconnaître les formes liées aux camions, car elles sont proches des voitures. Il faut donc avoir un « learning rate » plus faible pour éviter de détruire la cohérence du CNN d’origine !
Ensuite, il ne reste plus qu’à relancer l’entraînement du modèle avec les nouvelles données d’apprentissage… et voilà !
Conclusion partielle
La partie théorique s’arrête ici. Au vu de la longueur de ce focus, vous trouverez la partie « TP » dans un autre post dédié dont voici le lien.
TP sur le réseau de neurones convolutifs
Crédit de l’image de couverture : à la courtoisie des auteurs de l’article ResearGate en lien









[…] principe derrière un DCGAN est le suivant : en s’appuyant sur un réseau de neurones convolutifs, on va créer deux IA : une dont le rôle est de proposer des règles (ou des logos), et une dont […]
[…] cela fonctionne-t-il ? Si vous vous souvenez de notre focus sur les réseaux convolutifs, vous avez la solution : un réseau de neurones convolutifs, nommé VGG, a appris à générer un […]
[…] non 64 images… Pour plus de détails, n’hésitez pas à consulter notre tutoriel sur le réseau de neurones convolutifs ou son TP […]
[…] savoir plus : retrouvez notre tutoriel complet sur Pensée […]
[…] Lien vers le focus sur le CNN (convolutional neural network) […]
[…] L’application permet aussi à n’importe quel utilisateur de charger ses images de piège. Dans un premier temps elle trie les photos vides, puis identifie les espèces capturées. Pour ce faire, elle utilise un modèle basé sur un réseau de neurones convolutifs. […]