Un article qui sort de l’habituel puisqu’il est orienté Mathématiques… Non, restez, ce sera intéressant !
On vous propose de découvrir avec nous qu’est-ce qu’une distance, à quoi ça sert, avec plein d’exemples concrets et utiles. En particulier, nous verrons des distances applicables au langage, à la musique, ou à des groupements de personnes… Maîtrisez les notions derrière les algorithmes de machine learning, et choisissez la distance la plus adaptée à votre besoin !
Définition générale d’une distance
Si tout le monde sait mesurer la distance d’un point A à un point B avec une règle, il faut savoir que ce n’est pas la seule manière de procéder. Pour être appelée « distance », un système de mesure doit répondre à trois critères essentiels.
Notons \(E\) l’ensemble dans lequel on veut mesurer notre distance, qui est une application \(d :E\times E\to \mathbb{R}^+\).
La norme est une distance avec quelques propriétés supplémentaires, donc on confondra parfois les deux dans la suite de l’article sans que cela n’ait d’impact.
Symétrie
La distance du point A au point B doit être la même que la distance du point B au point A. Autrement dit, la distance n’a pas de sens.
Mathématiquement, cela s’écrit ainsi : \(\forall (a,b)\in E^2,\ d(a,b)=d(b,a)\)
Séparation
Cette propriété indique que si la distance de A à B vaut 0 alors, forcément, A = B (et inversement).
Aucun point ne peut être infiniment proche de A sans être A.
La formule est : \(\forall (a,b)\in E^2,\ d(a,b)=0 \Leftrightarrow a=b\)
Inégalité triangulaire
Aller de A à C est toujours plus court qu’aller de A à B puis de B à C.
Ainsi, ajouter une étape à notre chemin augmente sa longueur (ou au mieux la laisse inchangée) : \(\forall (a,b,c)\in E^3,\ d(a,c)\leq d(a,b)+d(b,c)\)
Exemples pratiques de distance
Mesure d’erreur ou de distance dans l’espace
Comparons 4 distances utilisées dans des espaces vectoriels (un plan dont on a l’habitude par exemple). Celles-ci servent essentiellement à mesurer l’écart entre une solution \(y_{prediction}\) trouvée par un algorithme de machine learning et la solution attendue \(y_{attendu}\) (on parle de l’erreur de notre algorithme).
Distance de Manhattan (norme \(L_1\))
Nommée ainsi car elle sert à « mesurer » la distance parcourue par une voiture dans la ville de Manhattan, elle est la plus simple : on additionne la distance parcourue sur chaque axe de l’espace (dans un plan, ce sera (en valeur absolue) la coordonnée en x + la coordonnée en y).
Il y a donc beaucoup de chemins qui ont la même longueur !
\(\sum_{i=1}^n |x_i-y_i|\).
Quand l’utiliser ?
- Si votre espace a beaucoup de dimensions, cette distance permet de converger plus vite. Dans cet article, les auteurs montrent qu’avec une dimension de 20, ils obtiennent une meilleure classification avec la distance de Manhattan (ou celles « inférieures ») plutôt qu’avec la distance euclidienne (ou celles « supérieures »)
- Si vous ne voulez pas accorder trop de crédit aux valeurs extrêmes : cette distance ne met pas du tout l’accent sur les fortes variations entre les composantes des vecteurs (on les additionne simplement)
Distance euclidienne (norme \(L_2\))
C’est la distance dont vous avez le plus l’habitude, celle de la règle, celle du « vol d’oiseau », la ligne droite. Sur notre schéma ci-dessus, c’est de mesurer la longueur du segment qui relie \(P_1\) à \(P_2\).
En voici la formule : \(\sqrt{\sum_{i=1}^n (x_i-y_i)^2}\).
Quand l’utiliser ?
- De manière générale, c’est la distance la plus utilisée car elle offre un bon compromis entre la gestion des valeurs faibles et celle des valeurs élevées
Distances d’ordre supérieur (norme \(L_p\) avec \(p \geq 1\))
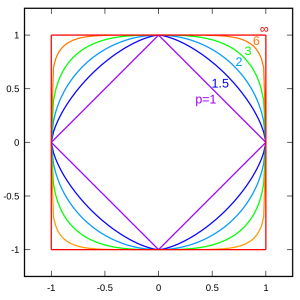
Il s’agit d’une généralisation des distances de Manhattan et euclidienne : on élève à une puissance p notre écart entre les coordonnées (p = 1 pour Manhattan et 2 pour Euclidienne), puis on prend la racine p-ième : \(\sqrt[p]{\sum_{i=1}^n |x_i-y_i|^p}\)
Dans l’exemple ci-contre, on voit à quoi ressemble le cercle unité (de rayon 1) lorsqu’on utilise ces distances.
Cette distance « p » est la distance de Minkowski.
Lorsque p tend vers l’infini, la distance devient une limite et on parle de distance de Tchebychev : \(\lim_{p \to \infty}\sqrt[p]{\sum_{i=1}^n |x_i-y_i|^p} = \sup_{1 \leq i \leq n}{|x_i-y_i|}\).
Quand les utiliser ?
- Etant une généralisation des normes \(L_1\) et \(L_2\), la réponse est simplement : « lorsque vous voulez donner de l’emphase aux valeurs élevées par rapport aux autres valeurs, ces normes ont tendance à ne garder que les grandes données ».
Distances fractionnaires (norme \(L_f\) avec \(f = \frac{1}{p}\))
Ces distances fractionnaires ne sont pas habituelles, même si elles sont l’autre partie de la généralisation des normes usuelles.
\(\sqrt[f]{\sum_{i=1}^n |x_i-y_i|^f}\) avec \(0 \leq f \leq 1\)
De manière générale, on peut généraliser à n’importe quel f fractionnaire, mais il faudra rester prudents.
Quand les utiliser ?
- Si les normes \(L_p\) accentuent les valeurs élevées, ces normes \(L_f\) font l’exact opposé : elles atténuent les valeurs extrêmes
- Il a également été démontré qu’utiliser ce type de distance dans des espaces à haute dimension permet d’accroître considérablement la convergence des algorithmes.
Par exemple, dans cet article, il est prouvé et observé que la norme \(L_0.1\), pour un espace à 20 dimensions, classifie les données à 99% contre 89% pour la norme \(L_2\) !
Distance entre les mots
Passons à présent aux distances utilisées pour du Natural Language Processing. Pour mesurer l’écart entre deux mots, plusieurs méthodes existent, mais la plus connue et la plus fréquente reste la distance de Levenshtein.
On se donne un ensemble d’actions élémentaires autorisées entres les mots M et P, qui ont chacune un coût de 1 :
- remplacer une lettre de M par une lettre de P (à la même place)
- ajouter dans M une lettre de P
- Supprimer dans M une lettre
Par exemple, pour passer de BONJOUR à BONSOIR, on pourrait supprimer J et U et mettre à la place S et I, ce qui représenterait une distance de 4, ou directement les substituer (distance de 2).
Remarque : la distance entre les deux mots est « la plus petite valeur » qu’on peut trouver (à la main) ! Il existe un algorithme qui donne systématiquement cette valeur, et c’est celui utilisé dans la pratique.
# Fonction récursive de la distance de Levenshtein
def LD(s, t):
# Cas d'arrêt
if s == "":
return len(t)
if t == "":
return len(s)
if s[-1] == t[-1]:
cost = 0
else:
cost = 1
# Récursion
res = min([LD(s[:-1], t)+1,
LD(s, t[:-1])+1,
LD(s[:-1], t[:-1]) + cost])
return res
# Exemple : la distance est de 3
print(LD("Python", "Peithen"))
Ce code, trouvé sur python-course n’est pas optimisé et de bien meilleures versions sont embarquées dans les librairies.
Quand l’utiliser ?
- Tout le temps, si on n’a pas de raison particulière d’utiliser une autre distance !
Une autre distance parfois utilisée est celle de Ratcliff/Obershelp : c’est le nombre de lettres qui sont plus ou moins au même emplacement (explication simplifiée, car en réalité on regarde la plus longue chaîne en commun puis on procède par récurrence dans les morceaux de mots que cela génère) entre les deux mots divisé par le nombre total de lettres (somme des deux mots).
Cette distance met donc l’accent sur les ressemblances des deux mots.
Par exemple, entre MATHEMATICS et MATEMATICA, la chaîne en commun la plus longue est EMATIC. Il nous reste MATH et S contre MAT et A. On compare d’abord MATH et MAT : la plus longue chaîne est MAT, il nous reste H mais on ne pourra rien en faire. De l’autre côté, on a S et A qui n’ont rien en commun.
On a donc trouvé 9 lettres en « commun » sur un total de 21 lettres. Comme elles sont en commun dans les deux mots, la distance RO entre ces deux mots est de 2*9/21 = 6/7.
Quand l’utiliser ?
- Cette distance a été inventée dans les années 80, essentiellement pour des besoins phonétiques. De plus, elle est coûteuse comparée à Levenshtein
- Elle est efficace pour trouver deux mots qui sont assez proches (faute de frappe)
Enfin, on va parler brièvement de la distance de Jaro-Winkler : celle-ci s’appuie sur la notion de transposition (inverser deux lettres de place) pour comparer les mots. L’algorithme complet est détaillé dans le lien, donc on ne va pas s’attarder dessus.
Quand l’utiliser ?
- Ici, on se concentre sur les fautes de frappe en fin de mot, car les utilisateurs se trompent rarement sur les premières lettres. Les mots SALUT et SALTU seront très proches, tandis que SALUT et TALUS seront éloignés (ce qui est compréhensible).
Distance entre les images
Ce sujet est très complexe et on trouve dans la littérature beaucoup de distances différentes dans leurs approches.
La manière la plus « traditionnelle » de procéder est de considérer son image comme une longue suite de 0 et de 1 (par exemple) en la mettant à plat. Ensuite, on utilise l’une des distances vue dans la partie sur les mots !
Sinon on peut également passer par des transformées de Fourier dont on compare les valeurs (on prend l’écart) coefficient à coefficient…
On peut aussi utiliser les vecteurs caractéristiques des images, des histogrammes… ou la distance de Hausdorff : utilisée habituellement pour des ensembles, elle se caractérise ainsi.
La distance de Hausdorff entre deux ensembles A et B est la plus grande des deux longueurs entre :
- Le point le plus éloigné de B qui est dans A ET B
- Le point le plus éloigné de A qui est dans B ET A
Sur l’image proposé par Wikipédia, A est le carré et B le cercle. La distance du point le plus éloigné du cercle qui est dans le carré est la longueur du segment a. De même, la distance entre un point du cercle et le carré est b au maximum.
La distance de Hausdorff sera donc le maximum entre a et b.
D’un point de vue mathématique, cela s’écrit (avec \(\delta\) la distance choisie pour mesurer « a » et « b », par exemple euclidienne) :
\(d(X,Y):=\max \; \{ \sup_{y\in Y} \delta(X,y), \quad \sup_{x\in X}\delta(x,Y)\}= \max \; \{ \sup_{y\in Y} \inf_{x \in X} \delta(x,y), \quad \sup_{x\in X} \inf_{y \in Y} \delta(x,y)\}.\)Quand l’utiliser ?
- Elle est très utilisée pour reconnaître les formes et numériser des images, de par sa nature
- Néanmoins, si deux formes ont des longueurs différentes, elle peut induire en erreur (il faut alors lui préférer la version modifiée)
- N’hésitez pas à consulter la page Wikipédia pour vous faire une autre idée de cette mesure très importante en traitement de l’image !
Distance entre les sons
La difficulté avec les sons est de passer d’une fonction continue à une fonction discrète. Si beaucoup de manières de procéder existent, il faut savoir que chacune d’entre elles aura un impact sur la distance calculée ensuite entre deux échantillons.
Dans cette partie, on va voir la distance de Hamming, simple mais utilisée constamment dans les codes correcteurs d’erreur.
La distance de Hamming entre deux suites de bits (de même longueur) est le nombre de bits qui diffèrent.
Par exemple, entre
1001 0101 et
1101 1011 on a en commun :
1X01 XXX1 la distance de Hamming est donc de 4 (il y a 4 bits qui ne correspondent pas).
Pour l’utiliser afin de mesurer l’écart entre deux échantillons sonores, Philips a proposé un système ingénieux qui consiste à découper le signal en bandes de fréquence qu’on hash ensuite (la fonction de hashage ne modifie que quelques bits avec le signal). De cette manière, on se retrouve avec deux empreintes de l’échantillon que l’on peut comparer. Celles-ci seront différentes si le signal n’est pas le même, et on pourra en mesurer l’écart.
Quand l’utiliser ?
- Lorsque vous voulez mesurer simplement l’écart entre deux fichiers audio
- Attention, car les séquences doivent être de même longueur
- Attention également au choix de la fonction de hashage !
Distance de permutations, dans le génome
La distance entre des permutations, que l’on va définir, sert principalement à mesurer le désordre présent dans une séquence.
Concrètement, si on se donne un ensemble de permutations, alors la distance entre deux permutations de cet ensemble est le plus petit nombre de transformations (permutations) qu’il faut réaliser pour passer de l’un à l’autre.
Par exemple,
1 2 3 4 5 6
4 3 1 2 6 5
Pour passer de 4 à 3 il faut deux permutations : 4 -> 2 -> 3. La distance entre les deux permutations est donc de 2. Pour passer de 5 à 6, il ne faut qu’une permutation (et inversement).
Vous retrouverez cette notion notamment lorsqu’on voudra évaluer l’efficacité d’un algorithme de tri (par rapport au désordre présent à l’origine dans notre liste), ou pour voir comment passer d’un génome à un autre. On peut aussi utiliser la distance de Kendal Tau.
Enfin, il existe aussi une distance génétique que nous n’aborderons pas ici car elle sert à mesurer l’écart entre deux locus d’un même chromosome.
Autres distances
On les abordera dans notre focus sur les K-Means : il existe plusieurs manières de mesurer la distance entre deux ensembles de points, en prenant par exemple la distance des deux points les plus éloignés des ensembles, les deux plus proches, les deux moyens à chaque ensemble, etc…
Crédit de l’image de couverture : RyanMcGuire – Pixabay License




[…] Suite à l’évaluation d’une entrée par le réseau de neurones, on peut la comparer à la réponse attendue et dire de combien est-ce qu’il s’est trompé. S’il prédit 0.7 et qu’on attendait 1, son erreur est calculée soit avec une norme (L_1) ou (L_2) ou autre (cf l’explication sur les normes). […]